题目内容
下列条件中,不能判断一个三角形是直角三角形的是
- A.三条边a、b、c满足a2+b2=c2
- B.三条边的比是1:2:3
- C.三个内角满足∠A-∠B=∠C
- D.三内角之比是1:2:3
B
分析:A、B根据勾股定理的逆定理进行判断;C、D根据三角形的内角和定理进行判断.
解答:A、三条边a、b、c满足a2+b2=c2符合勾股定理,故是直角三角形;
B、三条边的比为1:2:3,12+22≠32,故不是直角三角形;
C、三个角满足关系∠A-∠B=∠C,则∠A为90°,故是直角三角形;
D、三个角的比为1:2:3,设最小的角为x,则x+2x+3x=180°,x=30°,3x=90°,故是直角三角形.
故选B.
点评:本题考查的是勾股定理的逆定理,即如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.
分析:A、B根据勾股定理的逆定理进行判断;C、D根据三角形的内角和定理进行判断.
解答:A、三条边a、b、c满足a2+b2=c2符合勾股定理,故是直角三角形;
B、三条边的比为1:2:3,12+22≠32,故不是直角三角形;
C、三个角满足关系∠A-∠B=∠C,则∠A为90°,故是直角三角形;
D、三个角的比为1:2:3,设最小的角为x,则x+2x+3x=180°,x=30°,3x=90°,故是直角三角形.
故选B.
点评:本题考查的是勾股定理的逆定理,即如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
下列条件中,不能判断△ABC与△A′B′C′相似的是( )
| A、∠A=45°,∠C=26°,∠A′=45°,∠B′=109° | ||||||
B、AB=1,AC=
| ||||||
C、AB=1.5,AC=
| ||||||
D、AB=2,BC=1,∠C=90°,A′B′=
|
 4、如图所示,在下列条件中,不能判断△ABD≌△BAC的条件是( )
4、如图所示,在下列条件中,不能判断△ABD≌△BAC的条件是( )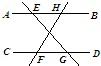 10、如图,下列条件中,不能判断直线AB∥CD的是( )
10、如图,下列条件中,不能判断直线AB∥CD的是( ) 如图,下列条件中,不能判断直线l1∥l2的是( )
如图,下列条件中,不能判断直线l1∥l2的是( )