题目内容
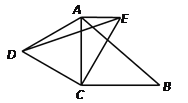
【题目】如图,在△ABC中,∠ ACB=90°BC=2,将△ACB绕点C逆时针旋转60°得到△DCE(A和D,B和E分别是对应顶点),若AE∥BC,则△ADE的周长为_________.
【答案】![]()
【解析】 根据旋转的性质得到CE=BC=2,AC=CD,∠BCE=∠ACD=60°,∠DCE=∠ACB=90°,推出△ACD是等边三角形,得到AD=AC,然后解直角三角形,由勾股定理即可得到结论.
∵将△ACB绕点C逆时针旋转60°得到△DCE,
∴CE=BC=2,AC=CD,∠BCE=∠ACD=60°,∠DCE=∠ACB=90°,
∴△ACD是等边三角形,
∴AD=AC,
∵AE∥BC,
∴∠EAC=90°,∠AEC=∠BCE=60°,
∴AE=![]() CE=1,AC=CD=
CE=1,AC=CD=![]() CE=
CE=![]() ,
,
∴DE=![]() ,
,
∴△ADE的周长=AE+AC+CE=1+![]() +
+![]() ,
,
故答案为:1+![]() +
+![]() .
.
“点睛”本题考查了旋转的性质,等边三角形的判定和性质,直角三角形的性质,平行线的性质,熟练掌握旋转的性质是解题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目