Question

在正方形ABCD中，点E是BC边的中点，过B点作BG⊥AE于点G，交AC于H，交CD于点F。（1）求证：点F为边BC的中点；（2）如果正方形的边长为4，求CH的长度；（3）如果点M是BC上的一点，且AM=MC+CD，
探究∠MAD与∠BAE有怎样的数量关系，说明理由。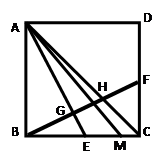

Answer 1

（1）证明：∵在正方形ABCD中，
∴AB=BC ∠ABC=∠BCD=90°
∵BG⊥AE
∴∠AGB=90°
∴∠ABG+∠BAG=90°
∠ABG+∠GBE=90°
∴ ∠BAG=∠GBE
∴△ABE≌△BCF   
∴BE="CF"
∵点E是BC边的中点 ∴BE=BC 
∴ CF=BC=CD   
∴点F为边BC的中点
（2）∵ AB="BC=4" , ∠ABC =90°     ∴AC=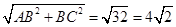
∵在正方形ABCD中, ∴AB∥CD ∴CH:HA=CF:AB
由(1)知CF=AB   ∴CH:HA=CF:AB=1:2
∴CH=AH=AC=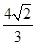       
（3）∠MAD=2∠BAE 理由如下：           
连接AF并延长交BC的延长线于点N,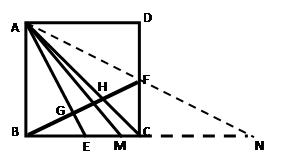

∵点F为边BC的中点     ∴可证△ADF≌△NCF
∴CN=AD，∠N= ∠CAN
∵在正方形ABCD中,  ∴AD=DC=DN，
∵ AM=MC+CD  ∴MC+CN="MC+CD=NM"
∴AM=MN    ∴∠N=∠MAN
∴∠MAD=2∠DAF
由（1）可知点F为CD的中点，
∴DF=BE  ∠ABE=∠ADF=90°   AB=AD
△ABE≌△ADF
∴∠DAF=∠BAE
∴∠MAD=2∠BAE                     

解析