题目内容
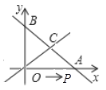
【题目】如图,点P是反比例函数![]() 上第一象限上一个动点,点A、点B为坐标轴上的点,A(0,k),B(k,0).已知△OAB的面积为
上第一象限上一个动点,点A、点B为坐标轴上的点,A(0,k),B(k,0).已知△OAB的面积为![]() .
.
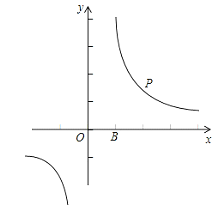
(1)求k的值;
(2)连接PA、PB、AB,设△PAB的面积为S,点P的横坐标为t.请直接写出S与t的函数关系式;
(3)阅读下面的材料回答问题:
当a>0时,![]()
∵![]() ≥0,∴
≥0,∴![]() ≥2,即
≥2,即![]() ≥2
≥2
由此可知:当![]() =0时,即a=1时,
=0时,即a=1时,![]() 取得最小值2.
取得最小值2.
问题:请你根据上述材料探索(2)中△PAB的面积S有没有最小值?若有,请直接写出S的最小值;若没有,说明理由.
【答案】(1) 1 (2) S=![]() ;(3)
;(3) ![]()
【解析】
(1)由双曲线过一三象限,则k>0,有三角形面积公式可求得k值;
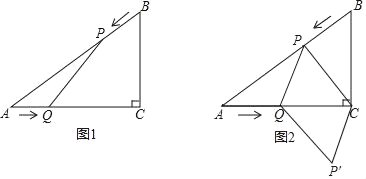
(2)过点P作PH⊥x轴于H,过点P作PG⊥y轴于G,连接OP,如图2.运用割补法就可解决问题;
(3)可借鉴阅读材料的经验,运用配方法就可解决问题.
(1)由图象可知:2k>0,即k>0,
则S△OAB=![]() OBOA=
OBOA=![]() k2=
k2=![]() ,
,
解得:k1=1,k2=-1,
∵k>0,
∴k=1;
(2)过点P作PH⊥x轴于H,过点P作PG⊥y轴于G,连接OP,如图2,
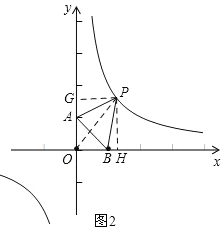
∵xP=t,
∴yP=![]() ,
,
∴PG=t,PH=![]() ,
,
则S=S四边形OAPB-S△OAB=S△OAP+S△OBP-S△OAB=![]() OAPG+
OAPG+![]() OBPH-
OBPH-![]() =
=![]() ×1×t+
×1×t+![]() ×1×
×1×![]() -
-![]() =
=![]() +
+![]() -
-![]() ,
,
∵点P在第一象限,
∴t>0,
∴S关于t的函数关系式为S=![]() +
+![]() -
-![]() ,t/span>的取值范围为t>0;
,t/span>的取值范围为t>0;
(3)S=![]() +
+![]() -
-![]() =
=![]() (t+
(t+![]() -1)=
-1)=![]() (t+
(t+![]() -2
-2![]() +2
+2![]() -1)=
-1)=![]() [(
[(![]() -
-![]() )2+2
)2+2![]() -1]=
-1]=![]() (
(![]() -
-![]() )2+
)2+![]() -
-![]() .
.
∴当![]() =
=![]() 即t=
即t=![]() 时,S取到最小值,最小值为
时,S取到最小值,最小值为![]() -
-![]() .
.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目