Question

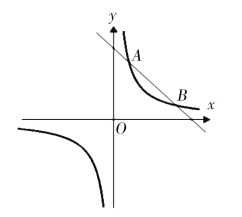
【题目】在平面直角坐标系中，抛物线与轴交于点（点在点的左侧），对称轴与轴交于点（3，0），且．

（1）求抛物线的表达式及顶点坐标；

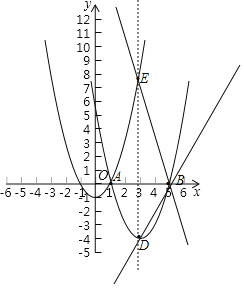
（2）将抛物线平移，得到的新抛物线的顶点为（0，﹣1），抛物线的对称轴与两条抛物线，围成的封闭图形为．直线经过点．若直线与图形有公共点，求的取值范围．

Answer 1

【答案】（1）抛物线的表达式为，抛物线的顶点为；（2）的取值范围是且．

【解析】

（1）利用对称轴与x轴交于点（3,0），AB=4,可得A、B坐标，将A、B坐标代入可得解析式，化成顶点式求得抛物线顶点坐标；

（2）利用平移后的的顶点为（0，﹣1）可得抛物线C2的解析式，易得抛物线的对称轴与抛物线的交点为，当直线过点和点时，代入可得，将和点代入可得，易得k的取值范围.

（1）∵抛物线的对称轴与轴交于点（3，0），

∴抛物线的对称轴为直线．

又∵，

∴．

∴

解得

∴抛物线的表达式为.

即．

∴抛物线的顶点为．

（2）∵平移后得到的新抛物线的顶点为，

∴抛物线的表达式为．

∴抛物线的对称轴与抛物线的交点为

①当直线过点和点时，

得

解得．

②当直线过点和点时，

得

解得

∴结合函数图象可知，的取值范围是且．