题目内容
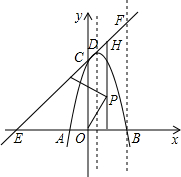 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交x轴于点E,过点B作x轴的垂线,交直线CD于点F,在坐标平面内找一点G,使以点G、F、C为顶点的三角形与△COE相似,请直接写出符合要求的,并在第一象限的点G的坐标;
(3)在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由;
(4)将抛物线沿其对称轴平移,使抛物线与线段EF总有公共点.试探究:抛物线向上最多可平移多少个单位长度?
分析:(1)设抛物线解析式为y=a(x+2)(x-4),把C的坐标代入即可求出a的值,再化成顶点式即可;
(2)求出C的坐标,过C作CG∥x轴交BF于G,根据C的坐标求出G坐标;当是(4,4)两三角形全等即相似,当是(8,8)时符合相似三角形的判定,即两三角形相似综合上述有3个点.
(3)设直线CD的解析式是y=kx+b,代入坐标后求出解析式,设P(2,t),根据距离相等列出方程求出即可;
(4)抛物线向上平移,可设解析式为y=-x2+2x+8+m,把x=4或-8代入即可列出不等式,即可求出答案.
(2)求出C的坐标,过C作CG∥x轴交BF于G,根据C的坐标求出G坐标;当是(4,4)两三角形全等即相似,当是(8,8)时符合相似三角形的判定,即两三角形相似综合上述有3个点.
(3)设直线CD的解析式是y=kx+b,代入坐标后求出解析式,设P(2,t),根据距离相等列出方程求出即可;
(4)抛物线向上平移,可设解析式为y=-x2+2x+8+m,把x=4或-8代入即可列出不等式,即可求出答案.
解答:解:(1)设抛物线解析式为y=a(x+2)(x-4),
把C(0,8)代入得a=-1,
∴y=-x2+2x+8=-(x-1)2+9,顶点D(1,9),
答:抛物线的解析式是:y=-x2+2x+8,顶点D的坐标是(1,9).
(2)G(4,8)或(8,8)或(4,4).
(3)假设满足条件的点P存在,依题意设P(2,t),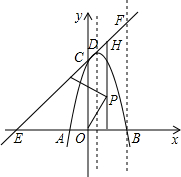
设直线CD的解析式是y=kx+b,
把C(0,8),D(1,9)代入得:
,
解得:
,
∴直线CD的解析式为:y=x+8,
它与x轴的夹角为45°,
设OB的中垂线交CD于H,则H(2,10).
则PH=|10-t|,点P到CD的距离为d=
PH=
|10-t|.
又PO=
=
.∴
=
|10-t|.
平方并整理得:t2+20t-92=0,t=-10±8
,
∴存在满足条件的点P,P的坐标为(2,-10±8
),
∴存在,点P的坐标是(2,-10+8
),(2,-10-8
),
(4)解:直线CD的解析式为:y=x+8,
当y=0时,x=-8,
当x=4时,y=12,
∴E(-8,0),F(4,12).
抛物线向上平移,可设解析式为y=-x2+2x+8+m(m>0).
当x=-8时,y=-72+m,
当x=4时,y=m,
∴-72+m≤0或m≤12,
∴0<m≤72.
∴向上最多可平移72个单位长,
答:抛物线向上最多可平移72个单位长度.
把C(0,8)代入得a=-1,
∴y=-x2+2x+8=-(x-1)2+9,顶点D(1,9),
答:抛物线的解析式是:y=-x2+2x+8,顶点D的坐标是(1,9).
(2)G(4,8)或(8,8)或(4,4).
(3)假设满足条件的点P存在,依题意设P(2,t),
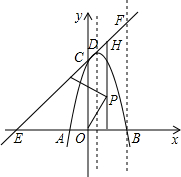
设直线CD的解析式是y=kx+b,
把C(0,8),D(1,9)代入得:
|
解得:
|
∴直线CD的解析式为:y=x+8,
它与x轴的夹角为45°,
设OB的中垂线交CD于H,则H(2,10).
则PH=|10-t|,点P到CD的距离为d=
| ||
| 2 |
| ||
| 2 |
又PO=
| t2+22 |
| t2+4 |
| t2+4 |
| ||
| 2 |
平方并整理得:t2+20t-92=0,t=-10±8
| 3 |
∴存在满足条件的点P,P的坐标为(2,-10±8
| 3 |
∴存在,点P的坐标是(2,-10+8
| 3 |
| 3 |
(4)解:直线CD的解析式为:y=x+8,
当y=0时,x=-8,
当x=4时,y=12,
∴E(-8,0),F(4,12).
抛物线向上平移,可设解析式为y=-x2+2x+8+m(m>0).
当x=-8时,y=-72+m,
当x=4时,y=m,
∴-72+m≤0或m≤12,
∴0<m≤72.
∴向上最多可平移72个单位长,
答:抛物线向上最多可平移72个单位长度.
点评:本题主要考查了二次函数图象与系数的特征,用待定系数法求一次函数的解析式,解一元二次方程和一元一次不等式,一次函数的点的坐标特征等知识点,解此题的关键是综合运用性质进行计算,此题综合性强,有一定的难度.

练习册系列答案
相关题目
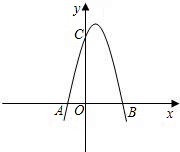 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).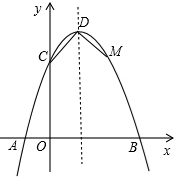 如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为x=1
如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为x=1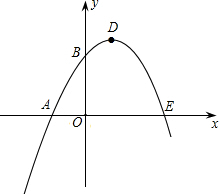 函数的最大值是4.
函数的最大值是4. (2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )
(2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )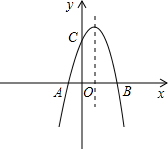 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).