Question

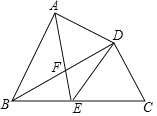
【题目】如图，在四边形ABCD中，对角线BD平分，，E为BC的中点，AE与BD相交于点F，若，则BF的长为（ ）

A.B.C.D.

Answer 1

【答案】C

【解析】

连接DE，结合直角三角形性质得出CD=DE=1，BC=2，BD=，AB=,然后利用角平分线性质证明出∠BDE=∠ABD，从而得出△AFB∽EFD，根据相似三角形对应边成比例进一步求解即可.

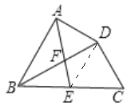
如图，连接DE，

∵，

∴△BDC是直角三角形，且∠C=60°，

∵E为BC的中点，

∴DE=BE=EC，

∴∠BDE=∠DBC=30°，

∴∠EDC=60°，

∴△DEC是等边三角形，

∴DE=EC=CD=1,

∴BC=2，

∴BD=，

∵BD平分，

∴∠ABD=∠DBC=30°，

∴AB=BD×cos30°=

∵∠BDE=∠DBC=30°，

∴∠BDE=∠ABD，

∴△ABF∽△EDF，

∴=，

∴BF=，

所以答案为C选项.