Question

【题目】如图，AD为△ABC的中线，BE为△ABD的中线．

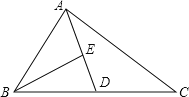
（1）∠ABE=15°，∠BAD=40°，求∠BED的度数；

（2）在△BED中作BD边上的高；

（3）若△ABC的面积为40，BD=5，则点E到BC边的距离为多少？

Answer 1

【答案】（1）55°；（2）见解析；（3）4

【解析】

试题分析：（1）根据三角形的一个外角等于与它不相邻的两个内角的和列式进行计算即可得解；

（2）根据高线的定义，过点E作BD的垂线即可得解；

（3）根据三角形的中线把三角形分成的两个三角形面积相等，先求出△BDE的面积，再根据三角形的面积公式计算即可．

解：（1）在△ABE中，∵∠ABE=15°，∠BAD=40°，

∴∠BED=∠ABE+∠BAD=15°+40°=55°；

（2）如图，EF为BD边上的高；

（3）∵AD为△ABC的中线，BE为△ABD的中线，

∴S△ABD=S△ABC，S△BDE=S△ABD，

∴S△BDE=S△ABC，

∵△ABC的面积为40，BD=5，

∴S△BDE=BDEF=×5EF=×40，

解得EF=4．