题目内容
9.若有理数a,b,c均不为0,且满足a+b+c=0,设x=$\frac{|a|}{b+c}$$+\frac{|b|}{c+a}$$+\frac{|c|}{b+a}$,则代数式x2-2013x+2014的值为2或4028.分析 根据题意,利用绝对值的代数意义确定出x的值,代入原式计算即可得到结果.
解答 解:∵a+b+c=0,
∴b+c=-a,c+a=-b,b+a=-c,
∴a,b,c中两个为负数或两个为正数,
∴当a,b,c中两个为负数时,x=1+1-1=1,此时原式=1-2013+2014=2;
当a,b,c中两个为正数时,x=1-1-1=-1,此时原式=1+2013+2014=4028,
故答案为:2或4028.
点评 此题考查了代数式求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
17. 如图,⊙O中,$\widehat{CA}=\widehat{CB}$,BD⊥AC于D,OC交BD于E.
如图,⊙O中,$\widehat{CA}=\widehat{CB}$,BD⊥AC于D,OC交BD于E.
(1)求证:∠BEO=∠A;
(2)若AB=4$\sqrt{2}$,OE=1,求⊙O的半径长.
 如图,⊙O中,$\widehat{CA}=\widehat{CB}$,BD⊥AC于D,OC交BD于E.
如图,⊙O中,$\widehat{CA}=\widehat{CB}$,BD⊥AC于D,OC交BD于E.(1)求证:∠BEO=∠A;
(2)若AB=4$\sqrt{2}$,OE=1,求⊙O的半径长.
1.比-4小2的数是( )
| A. | -2 | B. | -1 | C. | -6 | D. | 0 |
18.一个数的平方是16,则这个数的3次方是( )
| A. | 48 | B. | 64 | C. | -64 | D. | 64或-64 |
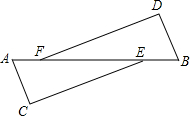 如图,A,F,E,B四点共线,AC⊥CE,BD⊥DF,AF=BE,AC=BD.AC∥BD,求证:FD=EC.
如图,A,F,E,B四点共线,AC⊥CE,BD⊥DF,AF=BE,AC=BD.AC∥BD,求证:FD=EC.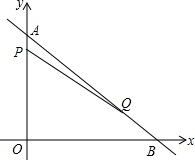 如图,在平面直角坐标系中,点A、点B分别在y轴、x轴的正半轴上,且满足$\sqrt{OA-30}$+(OB-40)2=0,若点P从A点出发,以每秒2个单位长度的速度沿线段AO运动,同时点Q从B点出发,以每秒5个单位长度的速度沿线段BA运动,连接PQ,点P,Q的运动时间为t秒.
如图,在平面直角坐标系中,点A、点B分别在y轴、x轴的正半轴上,且满足$\sqrt{OA-30}$+(OB-40)2=0,若点P从A点出发,以每秒2个单位长度的速度沿线段AO运动,同时点Q从B点出发,以每秒5个单位长度的速度沿线段BA运动,连接PQ,点P,Q的运动时间为t秒.