题目内容
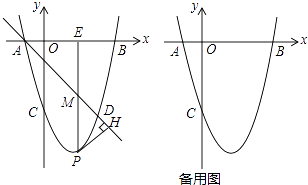
【题目】如图,在平面直角坐标系中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AO=BO=2,∠AOB=120°.
(1)求a,b的值;
(2)连结OM,求∠AOM的大小.
【答案】
(1)解:如图,过点A作AE⊥y轴于点E,
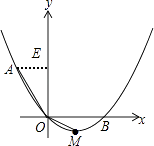
∵AO=OB=2,∠AOB=120°,
∴∠AOE=30°,
∴AE=1,EO= ![]() ,
,
∴A点坐标为:(﹣1, ![]() ),B点坐标为:(2,0),
),B点坐标为:(2,0),
将两点代入y=ax2+bx得:
![]() ,
,
解得:  .
.
∴a= ![]() ,b=﹣
,b=﹣ ![]()
(2)解:由(1)可知:抛物线的表达式为:y= ![]() x2﹣
x2﹣ ![]() x;
x;

过点M作MF⊥OB于点F,
∵y= ![]() x2﹣
x2﹣ ![]() x=
x= ![]() (x2﹣2x)=
(x2﹣2x)= ![]() (x﹣1)2﹣
(x﹣1)2﹣ ![]() ,
,
∴M点坐标为:(1,﹣ ![]() ),
),
∴tan∠FOM= ![]() =
= ![]() ,
,
∴∠FOM=30°,
∴∠AOM=30°+120°=150°
【解析】(1)如图,过点A作AE⊥y轴于点E,根据含30°的直角三角形的边之间的关系得出AE,OE的长,进而得出A,B两点的坐标,然后利用待定系数法就可以求出a,b的值;
(2)过点M作MF⊥OB于点F,根据抛物线求出其顶点M的坐标,从而得出OF,MF的长度,根据tan∠FOM的值就可以求出∠FOM的值,进而得出答案。

练习册系列答案
相关题目