题目内容
对于任意的两个实数对(a,b)和(c,d),规定:当a=c,b=d时,有(a,b)=(c,d);运算“?”为:(a,b)?(c,d)=(ac,bd);运算“⊕”为:(a,b)⊕(c,d)=(a+c,b+d).设p,q都是实数,如果(1,2)?(p,q)=(2,-4),
请计算:(1,2)⊕(p,q).
请计算:(1,2)⊕(p,q).
分析:先根据运算“?”求出p、q,然后根据运算“⊕”列式计算即可得解.
解答:解:∵(1,2)?(p,q)=(1•p,2q)=(2,-4),
∴p=2,q=-2,
∴(1,2)⊕(p,q)=(1,2)⊕(2,-2)=(1+2,2+(-2))=(3,0).
∴p=2,q=-2,
∴(1,2)⊕(p,q)=(1,2)⊕(2,-2)=(1+2,2+(-2))=(3,0).
点评:本题考查了有理数的除法,读懂题目信息理解两种运算“?”和“⊕”的运算方法是解题的关键.

练习册系列答案
相关题目
 和
和 ,规定:当
,规定:当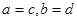 时,有
时,有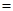
 ”为:
”为: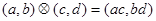 ;运算“
;运算“ ”为:
”为: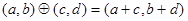 .设
.设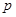 、
、 都是实数,若
都是实数,若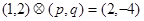 ,则
,则 .
.