题目内容
如图，在⊙O中，∠AOB的度数为160度，C是弧ACB上一点，D，E是弧AB上不同的两点（不与A，B两点重合），则∠D+∠E的度数为________．
100°
分析：首先连接OC，由在⊙O中，∠AOB的度数为160度，即可求得∠AOC+∠BOC=200°，然后根据在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半，即可求得∠D=
∠AOC，∠E=∠BOC，继而求得∠D+∠E的度数．
解答：
解：连接OC，
∵在⊙O中，∠AOB=160°，
∴∠AOC+∠BOC=360°-∠AOB=200°，
∵∠D=∠AOC，∠E=∠BOC，
∴∠D+∠E=∠AOC+∠BOC=（∠AOC+∠BOC）=100°．
故答案为：100°．
点评：此题考查了圆周角定理．此题难度适中，解题的关键是准确作出辅助线，掌握数形结合思想与整体思想的应用．
分析：首先连接OC，由在⊙O中，∠AOB的度数为160度，即可求得∠AOC+∠BOC=200°，然后根据在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半，即可求得∠D=
∠AOC，∠E=∠BOC，继而求得∠D+∠E的度数．解答：
解：连接OC，∵在⊙O中，∠AOB=160°，
∴∠AOC+∠BOC=360°-∠AOB=200°，
∵∠D=
∠AOC，∠E=∠BOC，∴∠D+∠E=
∠AOC+∠BOC=（∠AOC+∠BOC）=100°．故答案为：100°．
点评：此题考查了圆周角定理．此题难度适中，解题的关键是准确作出辅助线，掌握数形结合思想与整体思想的应用．
练习册系列答案
阅读快车系列答案
相关题目
19、如图，在△ABC中，CD⊥AB于D，FG⊥AB于G，ED∥BC，试说明∠1=∠2，以下是证明过程，请填空：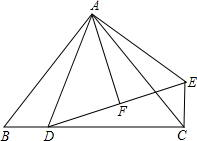
如图，在△ABC中，已知AB=AC，∠BAC=90°，D是BC上一点，EC⊥BC，EC=BD，DF=FE．求证：
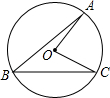如图，在⊙O中，∠ABC=40°，则∠AOC=
如图，在△ABC中，∠B，∠C的外角平分线相交于点O，若∠A=74°，则∠O=
15、如图，在△ABC中，AQ=PQ，PR=PS，PS⊥AC于S，PR⊥AB于R，则以下结论中：（1）AS=AR；（2）△BRP∽△QSP；（3）PQ∥AB中，正确的有