Question

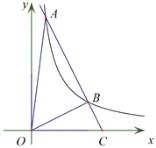
【题目】如图，、两点在反比例函数的图象上，、两点在反比例函数的图象上，轴于点，轴于点，，，，则的值是(　　)

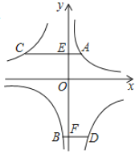
A.8B.6C.4D.10

Answer 1

【答案】A

【解析】

由反比例函数的性质可知S△AOE＝S△BOF＝k1，S△COE＝S△DOF＝﹣k2，结合S△AOC＝S△AOE+S△COE和S△BOD＝S△DOF+S△BOF可求得k1﹣k2的值．

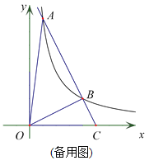
解：连接OA、OC、OD、OB，如图：

由反比例函数的性质可知S△AOE＝S△BOF＝|k1|＝k1，S△COE＝S△DOF＝|k2|＝﹣k2，

∵S△AOC＝S△AOE+S△COE，

∴ACOE＝×4OE＝2OE＝（k1﹣k2）…①，

∵S△BOD＝S△DOF+S△BOF，

∴BDOF＝×（EF﹣OE）＝×2（6﹣OE）＝6﹣OE＝（k1﹣k2）…②，

由①②两式解得OE＝2，

则k1﹣k2＝8．

故选：A．