��Ŀ����
����Ŀ����֪���κ���y=x2��2x+c��c��0����ͼ����x�ύ��A��B���㣨A����B�����ࣩ����y�ύ�ڵ�C����OB=OC��
��������������ߵĽ���ʽ�Ͷ������ꣻ
������ֱ��l�������ߵĶԳ��ᣬE�������ߵĶ��㣬����BE���߶�OC�ϵĵ�F����ֱ��l�ĶԳƵ�F��ǡ�����߶�BE�ϣ����F�����ꣻ
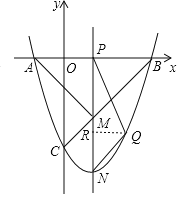
���������ж���P���߶�OB�ϣ�����P��x��Ĵ��߷ֱ���BC���ڵ�M���������߽��ڵ�N�����ʣ����������Ƿ���ڵ�Q��ʹ�á�PQN���APM�������ȣ����߶�NQ�ij�����С��������ڣ������Q�����ꣻ��������ڣ�˵�����ɣ�
���𰸡�����y=x2��2x��3����1����4����������F������Ϊ��0����2�������������ڣ���������ĵ�Q������Ϊ![]() ��
��![]() ��
��
��������������
��1������֪�����õ�C������Ϊ��0��c�������OB=OC����A�ڵ�B�����ɵõ�B������Ϊ��-c��0�����ѵ�B�����꣨-c��0������y=x2��2x+c�����c<0�������c��ֵ���Ӷ��õ������ߵĽ���ʽ�������ý���ʽ��Ϊ����ʽ���ɵõ������ߵĶ���������
��2���ɣ�1����֪�����ߵĶԳ���Ϊֱ��x=1�����F������Ϊ��0��m�������F�������Ϊ��2��m�����ɣ�1���ɵõ�B��E�����꣬���ɴ˿����ֱ��BE�Ľ���ʽ����F���������������BE�Ľ���ʽ�������m��ֵ���Ӷ��ɵô�ʱ��F�����ꣻ
��3������ͼ�����P������Ϊ��n��0������PA=n+1��PB=PM=3��n��PN=��n2+2n-3��
��QR��PN������ΪR����S��PQN=S��APM���ɵ�![]() ��n+1����3��n��=
��n+1����3��n��=![]() ����n2+2n+3��QR���������ɵ���QR=1��Ȼ��ֵ�Q��PN���Ҳ�������������ֱ��ú�n��ʽ�ӱ������R��N�����꣬Ȼ����Rt��QRN���ɹ��ɶ����ú�n��ʽ�ӱ����NQ2���������NQ��Сʱn��ֵ���ɴ˼��������Ӧ�ĵ�Q��������.
����n2+2n+3��QR���������ɵ���QR=1��Ȼ��ֵ�Q��PN���Ҳ�������������ֱ��ú�n��ʽ�ӱ������R��N�����꣬Ȼ����Rt��QRN���ɹ��ɶ����ú�n��ʽ�ӱ����NQ2���������NQ��Сʱn��ֵ���ɴ˼��������Ӧ�ĵ�Q��������.
��⣺
����y=x2��2x+c��c��0����
����C��������0��c����
��OB=OC����A�ڵ�B����࣬
����B����������c��0����
������c��0������y=x2��2x+c��
���c=��3��c=0����ȥ��
��c=��3��
�������ߵĽ���ʽΪy=x2��2x��3���䷽��y=��x��1��2��4��
������������1����4����
���������F��������0��m����
���Գ���Ϊֱ��l��x=1��
����F����ֱ�ߵĶԳƵ�F��������Ϊ��2��m����
��ֱ��BE�Ľ���ʽΪy=kx+b��
����1����֪��B��E������ֱ�Ϊ��3��0������1����4�����������������y=kx+b����
![]() �����
�����![]() ��
��
��ֱ��BE�Ľ���ʽΪy=2x��6��
����F����ֱ��BE�ϣ�
��m=2��2��6=��2��
����F��������0����2����
�����ڣ�
����ͼ��ʾ�����P������Ϊ��n��0����
��PA=n+1��PB=PM=3��n��PN=��n2+2n-3��
��QR��PN������ΪR��
��S��PQN=S��APM��
��![]() ��n+1����3��n��=
��n+1����3��n��=![]() ����n2+2n+3��QR��
����n2+2n+3��QR��
��QR=1��
����Q��ֱ��PN���Ҳ�ʱ��Q������Ϊ��n+1��n2��4����R�������Ϊ��n��n2��4����N�������Ϊ��n��n2��2n��3����
��QR=1��RN=2n-1��
����Rt��QNR��NQ2=1+��2n��1��2��
����n=![]() ʱ��NQȡ��Сֵ����ʱQ�������Ϊ
ʱ��NQȡ��Сֵ����ʱQ�������Ϊ![]() ��
��
����Q��ֱ��PN�����ʱ��Q�������Ϊ��n��1��n2��4n��
ͬ���ɵ���NQ2=1+��-2n+3��2��
����n=![]() ʱ��NQȡ��Сֵ����ʱQ�������Ϊ
ʱ��NQȡ��Сֵ����ʱQ�������Ϊ![]() ��
��
�������������������Q����Ϊ![]() ��
��![]() ��
��