Question

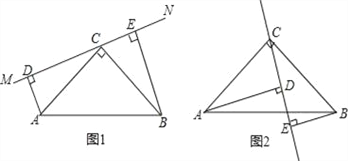
【题目】如图，直线AB、CD相交于O，OE⊥CD，且∠BOD的度数是∠AOD的5倍．

求：（1）∠AOD、∠BOD的度数；（2）∠BOE的度数．

Answer 1

【答案】(1) ∠AOD=30，∠BOD=150;(2) ∠BOE=60.

【解析】

(1)设∠AOD=x，则∠BOD=5x，列得x+5x=180，解出x即可得到答案；

（2）根据OE⊥CD，求出∠DOE=90，再用∠BOD-∠DOE即可得到∠BOE的度数.

(1)设∠AOD=x，则∠BOD=5x，

∵∠AOD+∠BOD=180，

∴x+5x=180，

x=30，

∴∠AOD=30，∠BOD=5x=150;

（2）∵OE⊥CD，

∴∠DOE=90，

∴∠BOE=∠BOD-∠DOE=150-90=60.