题目内容
设P是函数 在第一象限的图象上任意一点,点P关于原点的对称点为P′,过P作PA平行于y轴,过P′作P′A平行于x轴,PA与P′A交于A点,则△PAP′的面积( )
在第一象限的图象上任意一点,点P关于原点的对称点为P′,过P作PA平行于y轴,过P′作P′A平行于x轴,PA与P′A交于A点,则△PAP′的面积( )
A.等于2
B.等于4
C.等于8
D.随P点的变化而变化
【答案】分析:设P的坐标为(m,n),因为点P关于原点的对称点为P′,P′的坐标为(-m,-n);因为P与A关于x轴对称,故A的坐标为(m,-n);而mn=4,则△PAP′的面积为 •PA•P′A=2 mn=8.
•PA•P′A=2 mn=8.
解答:解:设P的坐标为(m,n),
∵P是函数 在第一象限的图象上任意一点,
在第一象限的图象上任意一点,
∴m•n=4.
∵点P关于原点的对称点为P′,
∴P'的坐标为(-m,-n);
∵P与A关于x轴对称,
∴A的坐标为(m,-n);
∴△PAP'的面积= •PA•P′A=2 mn=8.
•PA•P′A=2 mn=8.
故选C.
点评:本题结合反比例函数的性质考查了关于原点对称的点的坐标变化规律和关于x、y轴对称的点的性质,要注意二者的区别.
 •PA•P′A=2 mn=8.
•PA•P′A=2 mn=8.解答:解:设P的坐标为(m,n),
∵P是函数
 在第一象限的图象上任意一点,
在第一象限的图象上任意一点,∴m•n=4.
∵点P关于原点的对称点为P′,
∴P'的坐标为(-m,-n);
∵P与A关于x轴对称,
∴A的坐标为(m,-n);
∴△PAP'的面积=
 •PA•P′A=2 mn=8.
•PA•P′A=2 mn=8.故选C.
点评:本题结合反比例函数的性质考查了关于原点对称的点的坐标变化规律和关于x、y轴对称的点的性质,要注意二者的区别.

练习册系列答案
相关题目
 在第一象限的图象上任意一点,点P关于原点的对称点为P′,过P作PA平行于y轴,过P′作P′A平行于x轴,PA与P′A交于A点,则△PAP′的面积( )
在第一象限的图象上任意一点,点P关于原点的对称点为P′,过P作PA平行于y轴,过P′作P′A平行于x轴,PA与P′A交于A点,则△PAP′的面积( )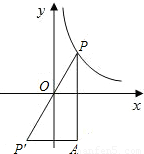
 在第一象限的图象上任意一点,点P关于原点的对称点为P′,过P作PA平行于y轴,过P′作P′A平行于x轴,PA与P′A交于A点,则△PAP′的面积( )
在第一象限的图象上任意一点,点P关于原点的对称点为P′,过P作PA平行于y轴,过P′作P′A平行于x轴,PA与P′A交于A点,则△PAP′的面积( )
 在第一象限的图象上任意一点,点P关于原点的对称点为P′,过P作PA平行于y轴,过P′作P′A平行于x轴,PA与P′A交于A点,则△PAP′的面积( )
在第一象限的图象上任意一点,点P关于原点的对称点为P′,过P作PA平行于y轴,过P′作P′A平行于x轴,PA与P′A交于A点,则△PAP′的面积( )
 在第一象限的图象上任意一点,点P关于原点的对称点为P′,过P作PA平行于y轴,过P′作P′A平行于x轴,PA与P′A交于A点,则△PAP′的面积( )
在第一象限的图象上任意一点,点P关于原点的对称点为P′,过P作PA平行于y轴,过P′作P′A平行于x轴,PA与P′A交于A点,则△PAP′的面积( )
 在第一象限的图象上任意一点,点P关于原点的对称点为P′,过P作PA平行于y轴,过P′作P′A平行于x轴,PA与P′A交于A点,则△PAP′的面积( )
在第一象限的图象上任意一点,点P关于原点的对称点为P′,过P作PA平行于y轴,过P′作P′A平行于x轴,PA与P′A交于A点,则△PAP′的面积( )