题目内容
如图，△ABC中，延长边AB、CA构成∠1，∠2，若∠C=55°，则∠1+∠2=
- A.125°
- B.235°
- C.250°
- D.305°
B
分析：根据外角的性质的∠1=∠BAC+55°，∠2=∠ABC+55°，则∠1+∠2=∠BAC+55°+∠ABC+55°=（∠BAC+∠C+∠ABC）+55°，根据三角形的内角和是180°求解．
解答：∵∠1=∠BAC+55°，∠2=∠ABC+55°，∠C=55°，
∴∠1+∠2=∠BAC+55°+∠ABC+55°=（∠BAC+∠C+∠ABC）+55°=180°+55°=235°．
故选B．
点评：此题利用了三角形内角和外角的关系，解答时要注意灵活运用三角形的内角和定理．
分析：根据外角的性质的∠1=∠BAC+55°，∠2=∠ABC+55°，则∠1+∠2=∠BAC+55°+∠ABC+55°=（∠BAC+∠C+∠ABC）+55°，根据三角形的内角和是180°求解．
解答：∵∠1=∠BAC+55°，∠2=∠ABC+55°，∠C=55°，
∴∠1+∠2=∠BAC+55°+∠ABC+55°=（∠BAC+∠C+∠ABC）+55°=180°+55°=235°．
故选B．
点评：此题利用了三角形内角和外角的关系，解答时要注意灵活运用三角形的内角和定理．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
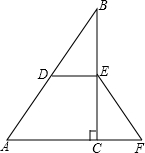如图，在△ABC中，∠ACB=90°，DE是△ABC的中位线，点F在AC延长上，且CF=
如图，在Rt△ABC中，AB=AC，∠BAC=90°，∠1=∠2，CE⊥BD的延长于E．求证：BD=2CE．
（2011•延平区质检）如图，RT△ABC中，∠ACB=90°，∠A=48°，将其折叠，使点A落在边CB上A′处，折痕为CD，则∠A′DB=（ ）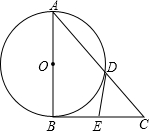
（2011•延平区质检）如图，RT△ABC中，∠ABC=90°，以AB为直径的⊙O交AC于点D，E为BC的中点，连接DE．
（2013•遵义）如图，在Rt△ABC中，∠ACB=90°，AC=BC=1，E为BC边上的一点，以A为圆心，AE为半径的圆弧交AB于点D，交AC的延长于点F，若图中两个阴影部分的面积相等，则AF的长为