题目内容
12.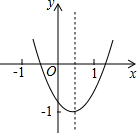 如图所示,二次函数y=ax2+bx+c的图象中,王慧同学观察得出了下面四条信息:
如图所示,二次函数y=ax2+bx+c的图象中,王慧同学观察得出了下面四条信息:(1)b2-4ac>0; (2)c>-1; (3)2a+b<0; (4)a+b+c<0,其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据抛物线与x轴的交点个数可判断(1),根据抛物线与y轴的交点位置可判断(2),根据对称轴在x=1的左侧可判断(3),根据x=1时y<0可判断(4).
解答 解:由图可知,抛物线与x轴有两个交点,
∴b2-4ac>0,故(1)正确;
∵抛物线与y轴的交点(0,c)在(0,-1)的上方,
∴c>-1,故(2)正确;
∵对称轴x=-$\frac{b}{2a}$<1,且a>0,
∴-b<2a,则2a+b>0,故(3)错误;
由图象知,当x=1时,y<0,即a+b+c<0,故(4)正确;
故选:C.
点评 此题考查了二次函数的图象与系数的关系.注意掌握二次项系数a决定抛物线的开口方向和大小,一次项系数b和二次项系数a共同决定对称轴的位置,常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c),抛物线与x轴交点个数确定△.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.方程x2-3x=0根是( )
| A. | x=-3 | B. | x1=0,x2=-3 | C. | x=3 | D. | x1=0,x2=3 |
17.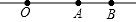 如图,下列不正确的说法是( )
如图,下列不正确的说法是( )
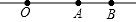 如图,下列不正确的说法是( )
如图,下列不正确的说法是( )| A. | 直线AB与直线BA是同一条直线 | B. | 射线OA与射线AB是同一条射线 | ||
| C. | 线段AB与线段BA是同一条线段 | D. | 射线OA与射线OB是同一条射线 |
2.下列二次根式中是最简二次根式的是( )
| A. | $\sqrt{4}$ | B. | $\sqrt{8}$ | C. | $\sqrt{10}$ | D. | $\sqrt{12}$ |
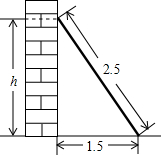 如图,长2.5m的梯子靠在墙上,梯子的底部离墙的底端1.5m,则梯子的顶端与地面的距离为2m.
如图,长2.5m的梯子靠在墙上,梯子的底部离墙的底端1.5m,则梯子的顶端与地面的距离为2m.