��Ŀ����
����ABCD�У�AD��BC����ABC=����0�㣼����90�㣩��AB=DC=3��BC=5����PΪ����BC�϶��㣨�����B��C�غϣ�����E��ֱ��DC�ϣ��ҡ�APE=�����ǡ�PAB=��1����EPC=��2��BP=x��CE=y��
��1������P���߶�BC��ʱ��д����֤����1���2��������ϵ��
��2�����ŵ�P���˶�����1���еõ��Ĺ��ڡ�1���2��������ϵ���Ƿ�ı䣿����Ϊ��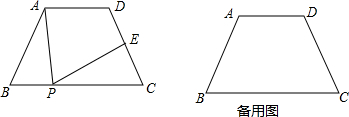 �ı䣬��֤��������Ϊ��ı䣬�������ͬ�ڣ�1����������ϵ����ָ����Ӧ��x��ȡֵ��Χ��
�ı䣬��֤��������Ϊ��ı䣬�������ͬ�ڣ�1����������ϵ����ָ����Ӧ��x��ȡֵ��Χ��
��3����cos��=
������x�Ĵ���ʽ��ʾy��
��1������P���߶�BC��ʱ��д����֤����1���2��������ϵ��
��2�����ŵ�P���˶�����1���еõ��Ĺ��ڡ�1���2��������ϵ���Ƿ�ı䣿����Ϊ��
 �ı䣬��֤��������Ϊ��ı䣬�������ͬ�ڣ�1����������ϵ����ָ����Ӧ��x��ȡֵ��Χ��
�ı䣬��֤��������Ϊ��ı䣬�������ͬ�ڣ�1����������ϵ����ָ����Ӧ��x��ȡֵ��Χ����3����cos��=
| 1 | 3 |
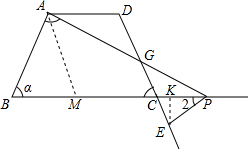
��������1����APC�ǡ�ABP����ǣ�������ǵ��ڲ����ڵ������ڽ�֮���á�1=��2��
��2����BP��5ʱ����1���2��������ϵ��Ȼ��ı䣮�����������ڽǺͶ������µĹ�ϵ��
��3�����������ηֱ���⣮�ٵ���P���߶�BC��ʱ�����ݡ�ABP�ס�PCE�ù�ϵ��⣻�ڵ���P���߶�BC���ӳ�����ʱ�����ݡ�EPC�ס�EGP�ù�ϵ��⣮
��2����BP��5ʱ����1���2��������ϵ��Ȼ��ı䣮�����������ڽǺͶ������µĹ�ϵ��
��3�����������ηֱ���⣮�ٵ���P���߶�BC��ʱ�����ݡ�ABP�ס�PCE�ù�ϵ��⣻�ڵ���P���߶�BC���ӳ�����ʱ�����ݡ�EPC�ס�EGP�ù�ϵ��⣮
��� ��1����1=��2
��1����1=��2
֤�����ߡ�APC=��ABC+��1���֡�APC=��APE+��2��
���ABC+��1=��APE+��2��
�ߡ�ABC=��=��APE�����1=��2
��2����ı䣬����P��BC�ӳ�����ʱ����x��5ʱ
��1���2��������ϵ��ͬ�ڣ�1����������ϵ��
�⣺�ߡ�APE=��=��ABC�����APB=��-��2��-------------------��1�֣�
�ߡ�ABC+��BAP+��APB=180�㣬���+��1+��-��2=180�㣬----��1�֣�
���1-��2=180��-2����-------------------------------------------------��1�֣�
��3���ٵ���P���߶�BC��ʱ��
�ߡ�1=��2����B=��C��
���ABP�ס�PCE��-------------------------------------------------------��1�֣�
��
=
��------------------------------------------------------------��1�֣�
��
=
����y=
x-
x2��------------------------------------��2�֣�
�ڵ���P���߶�BC���ӳ�����ʱ��
�ɵá�EPC�ס�EGP����EP2=EC•EG--------------------------��1�֣�
��AM��CD��
��AB=3��cos��=
��
��BM=2��
��GC=
(x-5)
��EK��BP����cos��=
��CK=
y��KE=
y����KP=x-5-
y
��EP2=(
y)2+(x-5-
y)2��
����y(y+
)=(
y)2+(x-5-
y)2
��y2+
(x-5)y=
y2+(x-5)2-
(x-5)y+
y2
�༴y=
-----------------------------------------------��2�֣�
 ��1����1=��2
��1����1=��2֤�����ߡ�APC=��ABC+��1���֡�APC=��APE+��2��
���ABC+��1=��APE+��2��
�ߡ�ABC=��=��APE�����1=��2
��2����ı䣬����P��BC�ӳ�����ʱ����x��5ʱ
��1���2��������ϵ��ͬ�ڣ�1����������ϵ��
�⣺�ߡ�APE=��=��ABC�����APB=��-��2��-------------------��1�֣�
�ߡ�ABC+��BAP+��APB=180�㣬���+��1+��-��2=180�㣬----��1�֣�
���1-��2=180��-2����-------------------------------------------------��1�֣�
��3���ٵ���P���߶�BC��ʱ��
�ߡ�1=��2����B=��C��
���ABP�ס�PCE��-------------------------------------------------------��1�֣�
��
| AB |
| PC |
| BP |
| CE |
��
| 3 |
| 5-x |
| x |
| y |
| 5 |
| 3 |
| 1 |
| 3 |
�ڵ���P���߶�BC���ӳ�����ʱ��
�ɵá�EPC�ס�EGP����EP2=EC•EG--------------------------��1�֣�
��AM��CD��
��AB=3��cos��=
| 1 |
| 3 |
��BM=2��
��GC=
| 3 |
| x-2 |
��EK��BP����cos��=
| 1 |
| 3 |
| 1 |
| 3 |
2
| ||
| 3 |
| 1 |
| 3 |
��EP2=(
2
| ||
| 3 |
| 1 |
| 3 |
����y(y+
| 3(x-5) |
| x-2 |
2
| ||
| 3 |
| 1 |
| 3 |
��y2+
| 3 |
| x-2 |
| 8 |
| 9 |
| 2 |
| 3 |
| 1 |
| 9 |
�༴y=
| 3x2-21x+30 |
| 2x+5 |
���������⿼���������й����������ε��ж������ʵ��ۺ�Ӧ�ã��ر��Ƕ�̬�����ۺ���ǿ���Ѷȴ�

��ϰ��ϵ�д�
 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�
�����Ŀ
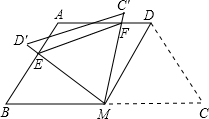 ��ͼ����������ABCD�У�AD��BC��AD=AB=CD=2����C=60�㣬M��BC���е㣮
��ͼ����������ABCD�У�AD��BC��AD=AB=CD=2����C=60�㣬M��BC���е㣮 DE��
DE�� ��ͼ��������ABCD�У�AD��BC��AB=CD����E��BC���ӳ����ϣ��ҡ�BDE=��ADC����֤��AB•BD=DE•AD��
��ͼ��������ABCD�У�AD��BC��AB=CD����E��BC���ӳ����ϣ��ҡ�BDE=��ADC����֤��AB•BD=DE•AD��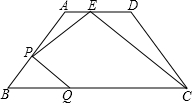 ��ͼ���ڵ�������ABCD�У�AD��BC��AB=5��AD=6��BC=12����E��AD���ϣ���AE��ED=1��2����P��AB���ϵ�һ�����㣬��P����A��B�غϣ�����P��PQ��CE��BC�ڵ�Q����AP=x��CQ=y����y��x֮��ĺ�����ϵ��
��ͼ���ڵ�������ABCD�У�AD��BC��AB=5��AD=6��BC=12����E��AD���ϣ���AE��ED=1��2����P��AB���ϵ�һ�����㣬��P����A��B�غϣ�����P��PQ��CE��BC�ڵ�Q����AP=x��CQ=y����y��x֮��ĺ�����ϵ�� �ֱ�CD��BC�ڵ�F��E����AD=3��BC=12��
�ֱ�CD��BC�ڵ�F��E����AD=3��BC=12��