Question

在平面直角坐标系xOy中，O′的坐标为（2，0），圆O′与x轴交于原点O和点A，一次函数y=tx+t（0＜t＜3）的图象与x轴y轴分别交于B、C两点
（1）圆O′与直线BC的位置关系如何；
（2）决定O′与直线BC位置的关键何在；
（3）直线BC的解析式能否确定？

Answer 1

解：（1）根据圆O′与x轴交于原点O和点A，画出图象，可以得出一次函数y=tx+t（0＜t＜3）的图象与x轴y轴分别交于B、C两点，B点坐标为：（-1，0），C点坐标为：（0，t），
当直线BC与圆O′相切，切点为E，连接O′E，则EO′=2，EO′⊥BE，
∵∠CBO=∠CBO′，∠BOC=∠BEO′，
∴△BOC∽△BEO′，
∴=，
利用BE=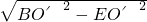==，BO=1，
解得：CO=，
即t=，
由于0＜t＜3，
故圆O′与直线BC的位置关系有3种相切，相交，相离；

（2）根据（1）中所求可以得出决定O′与直线BC位置的关键在于t的取值；

（3）由于t的值不知道，且直线与圆的位置关系无法确定，故得出直线BC的解析式不能确定．
分析：（1）根据已知得出B点坐标，再利用相似三角形的判定与性质得出t的值，进而分析得出答案即可；
（2）利用（1）中所求可以得出决定O′与直线BC位置的关键在于t的取值；
（3）由于t的值不知道，且直线与圆的位置关系无法确定，故直线BC的解析式不能确定．
点评：此题主要考查了一次函数的综合应用以及直线与圆的位置关系，根据已知得出相切时t的值是解题关键．