题目内容
如图，AB=AC，FD⊥BC于D，DE⊥AB于E，若∠AFD=145°，求∠EDF的度数．
解：∵AB=AC，
∴∠B=∠C，
∵FD⊥BC于D，DE⊥AB于E，
∴∠BED=∠FDC=90°，
∵∠AFD=145°，
∴∠EDB=∠CFD=180°-145°=35°，
∴∠EDF=90°-∠EDB=90°-35°=55°．
故∠EDF的度数是55°．
分析：先根据等腰三角形等边对等角的性质得到∠B=∠C，利用等角的余角相等和已知角可求出∠EDB的数，从而可求得∠EDF的度数．
点评：本题综合考查等腰三角形，三角形外角性质等知识．一般是利用等腰三角形的性质得出有关角的度数，进而求出所求角的度数．
∴∠B=∠C，
∵FD⊥BC于D，DE⊥AB于E，
∴∠BED=∠FDC=90°，
∵∠AFD=145°，
∴∠EDB=∠CFD=180°-145°=35°，
∴∠EDF=90°-∠EDB=90°-35°=55°．
故∠EDF的度数是55°．
分析：先根据等腰三角形等边对等角的性质得到∠B=∠C，利用等角的余角相等和已知角可求出∠EDB的数，从而可求得∠EDF的度数．
点评：本题综合考查等腰三角形，三角形外角性质等知识．一般是利用等腰三角形的性质得出有关角的度数，进而求出所求角的度数．
练习册系列答案
相关题目
24、如图，AB=AC=AD．
（2012•虹口区一模）已知：如图，AB=AC，∠DAE=∠B．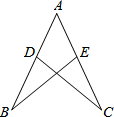
（2013•来宾）如图，AB=AC，D，E分别是AB，AC上的点，下列条件中不能证明△ABE≌△ACD的是
如图，AB=AC，∠C=67°，AB的垂直平分线EF交AC于点D，求∠DBC的度数．
如图，AB=AC=10，∠A=40°，AB的垂直平分线MN交AC于点D，求：