Question

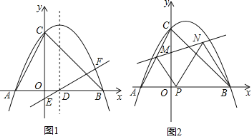
【题目】如图，已知抛物线＝与轴交于、两点，与轴交于点，且＝．

（1）求抛物线的函数表达式；

（2）若点是线段上的一个动点（不与、重合），分别以、为一边，在直线的同侧作等边三角形和，求的最大面积，并写出此时点的坐标；

（3）如图，若抛物线的对称轴与轴交于点，是抛物线上位于对称轴右侧的一个动点，直线与轴交于点．是否存在点，使与相似？若存在，请求出点的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）；（2），(1，0)；（3）存在，、、或

【解析】

（1）令x=0得，y=4，求出点C（0，4），根据OB=OC=4，得到点B（4，0）代入抛物线表达式求出a的值，即可解答；

（2）过点M作MG⊥x轴于G，过点N作NH⊥x轴于H，设P（x，0），△PMN的面积为S，分别表示出，，，，根据＝，利用二次函数的性质当x=1时，S有最大值是，此时点的坐标是；

（3）存在点F，使得△DOE与△AOC相似．有两种可能情况：①△DOE∽△AOC；②△DOE∽△COA，先求出点E的坐标，再求出直线DE的解析式，利用方程组求出点F的坐标，即可解答．

解：（1）令＝得，＝，

∴，

∴＝＝，

∴，

代入抛物线表达式得：

＝，解得，

∴抛物线的函数表达式为，

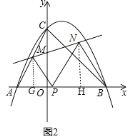
（2）如图，过点作轴于，过点作轴于，

由抛物线得：，

设，的面积为，

则，，，，

∴＝，

S，

∵，

∴当＝时，有最大值是，

∴的最大面积是，此时点的坐标是，

（3）存在点，使得与相似．有两种可能情况：①；②，

由抛物线得：，对称轴为直线＝，

∴＝，＝，＝，

①若，则，

∴，

解得＝，

∴点的坐标是或，

若点的坐标是，

则直线为：＝，

解方程组，

得：，（不合题意，舍去），

此时满足条件的点的坐标为，

若点的坐标是，

同理可求得满足条件的点的坐标为，

②若，

同理也可求得满足条件的点的坐标为，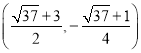

满足条件的点的坐标为，

综上所述，存在满足条件的点，点的坐标为：

、、或．