题目内容
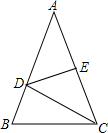如图，等腰△ABC中，AB=AC=10，AC的垂直平分线DE交AB于D，交AC于E，BC=6，则△CDB的周长为________．
16
分析：由AC的垂直平分线DE交AB于D，交AC于E，根据线段垂直平分线的性质，即可求得AD=CD，又由△CDB的周长为：BC+CD+BD=BC+AD+BD=BC+AB，即可求得答案．
解答：∵DE是AC的垂直平分线，
∴AD=CD，
∵等腰△ABC中，AB=AC=10，BC=6，
∴△CDB的周长为：BC+CD+BD=BC+AD+BD=BC+AB=6+10=16．
故答案为：16．
点评：此题考查了线段垂直平分线的性质．此题比较简单，注意数形结合思想与转化思想的应用．
分析：由AC的垂直平分线DE交AB于D，交AC于E，根据线段垂直平分线的性质，即可求得AD=CD，又由△CDB的周长为：BC+CD+BD=BC+AD+BD=BC+AB，即可求得答案．
解答：∵DE是AC的垂直平分线，
∴AD=CD，
∵等腰△ABC中，AB=AC=10，BC=6，
∴△CDB的周长为：BC+CD+BD=BC+AD+BD=BC+AB=6+10=16．
故答案为：16．
点评：此题考查了线段垂直平分线的性质．此题比较简单，注意数形结合思想与转化思想的应用．
练习册系列答案
相关题目
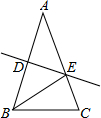如图，等腰△ABC中，AB=AC，∠A=20°．线段AB的垂直平分线交AB于D，交AC于E，连接BE，则∠CBE等于（ ）| A、80° | B、70° | C、60° | D、50° |
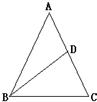13、如图，等腰△ABC中，AB=AC，BD为腰AC的中线，将△ABC分成长12cm和9cm的两段，则等腰△ABC的腰长为
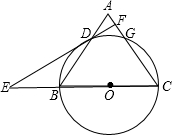如图，等腰△ABC中，AC=BC=10，AB=12，以BC为直径作⊙0交AB于D，交AC于G，DF⊥AC，垂足为F，交CB的延长线于点E，则sinE=
如图，等腰△ABC中，AB=AC，D为BC中点，E为射线AD上一点．
如图，等腰△ABC中，AB=AC，D、E分别为AC、AB的中点．