题目内容
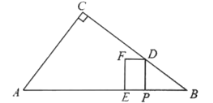
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,以每秒3个单位长度的速度向终点
出发,以每秒3个单位长度的速度向终点![]() 运动,过点
运动,过点![]() 作
作![]() 交
交![]() 边或
边或![]() 边于点
边于点![]() ,点
,点![]() 是射线
是射线![]() 边上一点,总保持
边上一点,总保持![]() ,以
,以![]() 、
、![]() 为邻边构造矩形
为邻边构造矩形![]() ,设矩形
,设矩形![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() .
.
(1)用含![]() 的式子表示线段
的式子表示线段![]() 的长;
的长;
(2)当点![]() 落在
落在![]() 上时,求
上时,求![]() 的值;
的值;
(3)当矩形![]() 与
与![]() 重叠部分图形为四边形时,求
重叠部分图形为四边形时,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(4)点![]() 与点
与点![]() 同时出发,在线段
同时出发,在线段![]() 上以每秒5个单位长度的速度沿
上以每秒5个单位长度的速度沿![]() 往返一次,连结
往返一次,连结![]() 、
、![]() ,直接写出矩形
,直接写出矩形![]() 的面积是
的面积是![]() 的面积的2倍时
的面积的2倍时![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;(4)
;(4)![]() ,
,![]() ,
,![]() .
.
【解析】
(1)由题意可知:![]() ,PB=3t,据此解答即可;
,PB=3t,据此解答即可;
(2)先根据勾股定理求出AC的长,当点![]() 落在
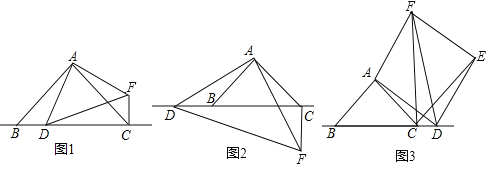
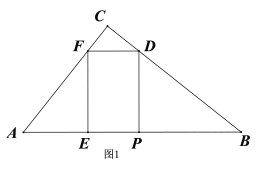
落在![]() 上时,如图1,在Rt△DPB中先利用∠A的正切用含t的代数式表示出DP,即为EF,再在Rt△AEF中利用三角函数的知识用含t的关系式表示出AE,由AE+EP+PB=5可得关于t的方程,解方程即得结果;
上时,如图1,在Rt△DPB中先利用∠A的正切用含t的代数式表示出DP,即为EF,再在Rt△AEF中利用三角函数的知识用含t的关系式表示出AE,由AE+EP+PB=5可得关于t的方程,解方程即得结果;
(3)当![]() 时,根据(2)题的结果利用三角形的面积公式直接解答即可;当C、D重合时,如图2,当A、E两点重合时,如图3,分别求出这两种情况t的值,进而可得矩形
时,根据(2)题的结果利用三角形的面积公式直接解答即可;当C、D重合时,如图2,当A、E两点重合时,如图3,分别求出这两种情况t的值,进而可得矩形![]() 与
与![]() 重叠部分图形为四边形时t的范围,再结合图4利用三角函数的知识用含t的代数式表示出DP和RE,然后根据梯形的面积公式解答即可;
重叠部分图形为四边形时t的范围,再结合图4利用三角函数的知识用含t的代数式表示出DP和RE,然后根据梯形的面积公式解答即可;
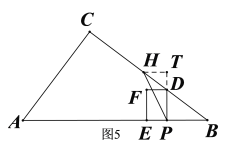
(4)分H、D重合之前,如图5;H、D重合以后,D、H仍在BC边上,如图6;点D在AC边上、点H在BC边上,如图7共三种情况,先利用三角函数的知识用含t的代数式表示出DP边上的高HT的长,再根据矩形![]() 的面积是
的面积是![]() 的面积的2倍即可列出关于t的方程,解方程即可求得结果.
的面积的2倍即可列出关于t的方程,解方程即可求得结果.
解:(1)∵![]() ,PB=3t,
,PB=3t,
∴![]() ;
;
(2)在![]() 中,∵
中,∵![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,
当点![]() 落在
落在![]() 边上时,如图1,在Rt△DPB中,
边上时,如图1,在Rt△DPB中,![]() ,
,
∵四边形![]() 是矩形,∴EF=DP
是矩形,∴EF=DP![]() ,
,
在Rt△AEF中,![]() ,
,
∵AE+EP+PB=5,
∴![]() ,解得:
,解得:![]() ;
;
(3)当![]() 时,重合部分为四边形,由(2)题知:
时,重合部分为四边形,由(2)题知:![]() ;
;
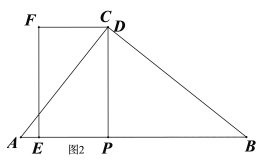
当C、D重合时,如图2,此时重合部分为四边形,![]() ,即
,即![]() ,解得:
,解得:![]() ,
,
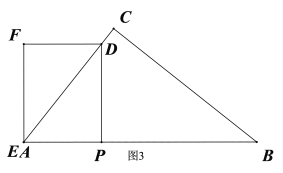
当A、E两点重合时,如图3,此时重合部分为三角形,AP=![]() ,由AP+BP=5,得
,由AP+BP=5,得![]() ,解得:
,解得:![]() ,
,
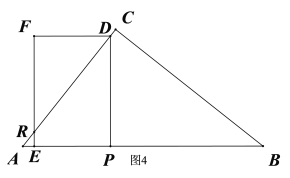
∴当![]() 时,如图4,
时,如图4,![]() ,
,
∴![]() ;
;
∴当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ;
;
(4)①当H、D重合之前,由题意知CH=5t,![]() ,∴
,∴![]() ,
,
于是当![]() 时,过点H作HT⊥PD交PD延长线于点T,如图5,则
时,过点H作HT⊥PD交PD延长线于点T,如图5,则![]() ,
,
若矩形![]() 的面积是
的面积是![]() 的面积的2倍,则
的面积的2倍,则![]() ,
,
解得:![]() ,或t=0(舍去);
,或t=0(舍去);
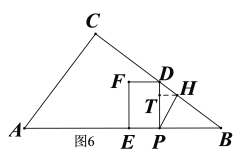
②当H、D重合以后,D、H仍在BC边上,如图6,此时![]() ,
,![]() ,
,
若矩形![]() 的面积是
的面积是![]() 的面积的2倍,则
的面积的2倍,则![]() ,
,
解得:![]() ,或t=0(舍去);
,或t=0(舍去);
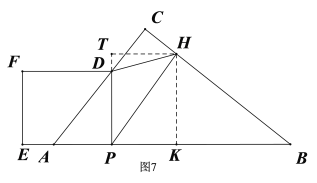
③当点D在AC边上、点H在BC边上时,即![]() ,如图7,作HK⊥AB于点K,则
,如图7,作HK⊥AB于点K,则![]() ,
,![]() ,
,
若矩形![]() 的面积是
的面积是![]() 的面积的2倍,则
的面积的2倍,则![]() ,
,
即![]() ,解得:
,解得:![]() .
.
综上所述:若矩形![]() 的面积是
的面积是![]() 的面积的2倍,t=
的面积的2倍,t=![]() 或
或![]() 或
或![]() .
.

【题目】某印刷厂的打印机每5年需淘汰一批旧打印机并购买新机,买新机时,同时购买墨盒,每盒150元,每台新机最多可配买24盒;若非同时配买,则每盒需220元.
公司根据以往的记录,十台打印机正常工作五年消耗墨盒数如表:
消耗墨盒数 | 22 | 23 | 24 | 25 |
打印机台数 | 1 | 4 | 4 | 1 |
(1)以这十台打印机消耗墨盒数为样本,估计“一年该款打印机正常工作5年消耗的墨盒数不大于24”的概率;
(2)试以这10台打印机5年消耗的墨盒数的平均数作为决策依据,说明购买10台该款打印机时,每台应统一配买23盒墨还是24盒墨更合算?