题目内容
【题目】如图，矩形
矩形
，
、
分别为它们的短边，点
在
上，
．
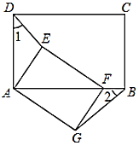
（1）求证：
．
（2）若两个矩形的面积之和为
，求矩形的面积．
【答案】（1）见解析；（2）矩形ABCD的面积为450
【解析】
（1）利用相似多边形的性质得到AE:AD=AG:AB，然后证得∠DAE=∠GAB，从而得到△ADE∽△ABG，利用相似三角形的对应角相等即可求得结论；
（2）首先利用相似多边形的对应边的关系得到相似比，从而利用面积的比等于相似比的平方求得结论.
解：（1）∵四边形ABCD为矩形，四边形AEFG∽四边形ADCB，
∴
，
，
∴
，
∴
，
∵，
∴
，
∴
．
（2）∵3AE=2AD，
∴
，
∵矩形AGFE∽矩形ABCD，
∴相似比为，
∴面积的比为
，
∴
，
又∵
，
∴
=200，
=450.
即矩形ABCD的面积为450.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
