Question

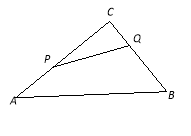
【题目】已知：如图，在△ABC中，AB=AC且tanA= ，P为BC上一点，且BP：PC=3：5，E、F分别为AB、AC上的点，且∠EPF=2∠B，若△EPF的面积为6，则EF=________．

Answer 1

【答案】2

【解析】

由∠B=∠C、∠A+∠B+∠C=180°,知∠A+2∠B=180°，由∠β=2∠B得∠A+∠β=180°，根据四边形内角和得∠3+∠4=180°，继而由∠4+∠1=180°知∠3=∠1，再分两种可能：①∠3=∠4=90°，结合∠B=∠C可得△PBE∽△PFC，从而得知 ②∠3≠∠4，以P为圆心，PF为半径画弧交CF于点G，证△PBE∽△PCG得作FD⊥EP，由∠β+∠A=∠β+∠α=180°知∠A=∠α，从而得tanA=tanα= 故可设FD=4x，则PD=3x，求出PF=PG=5x，PE=3x，根据,可得x的值，从而得出DE、DF的长，即可得答案．

∵AB=AC，

∴∠B=∠C，

∵

∴

如图所示，

∵∠β=∠EPF=2∠B，

∴

∵

∴

∵

∴∠3=∠1，

若

∵∠B=∠C，

∴△PBE∽△PFC，

∴

若∠3≠∠4，不放设∠4>∠3，则可以P为圆心，PF为半径画弧交CF于点G，

∴PF=PG，

∴∠1=∠2，

∵∠3=∠1，

∴∠3=∠2，

∴∠5=∠6，

∴△PBE∽△PCG，

∴

作FD⊥EP于点D，

∵

∴∠A=∠α，

∵tanA=tanα=

设FD=4x,则PD=3x,(x>0)，

由勾股定理得PF=5x，即PG=5x，

∵

∴PE=3x，

∴

∵

∴

解得：x=1或x=1(舍)，

∴DE=6x=6，DF=4x=4，

由勾股定理可得

故答案为：