Question

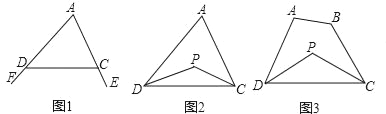
【题目】如图①，已知是⊙的直径， 是上的一个动点（点与点、不重合），连接． 是的中点，作弦，垂足为．

（）若点和点不重合，连接、和．当是等腰三角形时，求的度数．

（）若点和点重合，如图②．探索与的数量关系并说明理由．

Answer 1

【答案】（）（）

【解析】试题分析：（）如图，设， ，由是等腰三角形，可得，从而得，得到，再由是的中点，可得，从而得，得，由是直径，可得①，根据，可得，即②，解方程组即可得；

（）设，由已知可得， ，再由三角形内和定理可得，从而得， 中，根据勾股定理即可得．

试题解析：（）如图，设， ，

∵是等腰三角形，∴，∴，∴，

∵， ，∴，

∵是的中点，∴，∴，∴，

∵是直径，∴，∴①，

∵，∴，∴，即②，

，解得，即；

（）设，由于是的中点，∴，

∵，∴是的垂直平分线，∴，

∵，即，∴，

∵是直径，∴， 中： ，

，∴．