Question

如图，抛物线y=ax²+bx+c的对称轴为直线x=-3，该抛物线交x轴于A、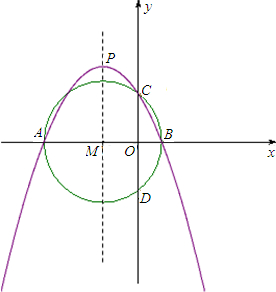B两点，交y轴于点C（0，4），以AB为直径的⊙M恰好经过点C．
（1）求这条抛物线所对应的函数关系式；
（2）设⊙M与y轴的另一个交点为D，请在抛物线的对称轴上求作一点E，使得△BDE的周长最小，并求出点E的坐标；
（3）过点C作⊙M的切线CF交x轴于点F，试判断直线CF是否经过抛物线的顶点P？并说明理由．

Answer 1

分析：（1）连接MC．在Rt△MCO中，由勾股定理得MC=5，故可求出A、B两点的坐标，由A、B、C三点的坐标即可求出这条抛物线所对应的函数关系式；
（2）连接AD交抛物线的对称轴于点E，则点E即为所求作的点，由A、D两点的坐标可求出直线AD所对应的函数关系式，进而可求出E点坐标；
（3）由于直线CF为⊙O的切线，故∠MCF=90°，再根据∠OMC=∠CMF可知Rt△OMC∽Rt△CMF，由相似三角形的性质可求出MF的长，进而可得出CF所对应的函数关系，由（1）中所求抛物线的解析式求出其顶点坐标，把其顶点坐标代入直线CF的解析式看是否适合即可．

解答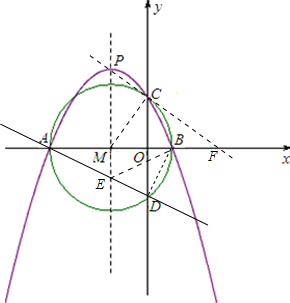：解：（1）连接MC．在Rt△MCO中，由勾股定理得MC=5．（1分）
∴MA=MB=5，∴A（-8，0）、B（2，0），
由A（-8，0）、B（2，0）、C（0，4）可求得这条抛物线所对应的函数关系式为y=-

1

4

x²-

3

2

x+4；

（2）连接AD交抛物线的对称轴于点E，则点E即为所求作的点，
由A（-8，0）、D（0，-4）可求得直线AD所对应的函数关系式为y=-

1

2

x-4，
当x=-3时，y=-

5

2

，
∴点E的坐标为（-3，-

5

2

）；（6分）

（3）∵直线CF为⊙O的切线，
∴∠MCF=90°．
又∵∠OMC=∠CMF，
∴Rt△OMC∽Rt△CMF．
∴

OM

CM

=

MC

MF

，即

3

5

=

5

MF

．
解得MF=

25

3

．
∴OF=

16

3

，
∴F（

16

3

，0），
由C（0，4）、F（

16

3

，0）可求得直线CF所对应的函数关系式为：y=-

3

4

x+4，
又∵y=-

1

4

x²-

3

2

x+4=-

1

4

（x+3）²+

25

4

，
∴抛物线的顶点P（-3，

25

4

），
经检验，点P（-3，

25

4

）在直线CF：y=-

3

4

x+4上，即直线CF经过抛物线的顶点P．

点评：本题考查的是二次函数综合题，涉及到用待定系数法求一次函数及二次函数的解析式，相似三角形的判定与性质等相关知识，难度较大．