题目内容
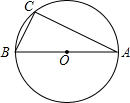
如图，AB是半圆O的直径，C为半圆上一点，∠CAB的角平分线AE交BC于点D，交半圆O于点E．若AB=10，tan∠CAB=
，求线段BC和CD的长．
| 3 |
| 4 |
∵AB是半圆O的直径，
∴∠C=90°．
∵tan∠CAB=
，
∴
=
．
设AC=4k，BC=3k，
∵AC2+BC2=AB2，AB=10，
∴（4k）2+（3k）2=100．
∴k1=2，k2=-2（舍去）．
∴AC=8，BC=6．
过点D作DF⊥AB于F，
∵AD是∠CAB的角平分线，
∴CD=DF．
∵∠DFB=∠ACB=90°，∠DBF=∠ABC，
∴△DBF∽△ABC．
∴
=
．
即
=
．
∴CD=
．
∴∠C=90°．
∵tan∠CAB=
| 3 |
| 4 |
∴
| BC |
| AC |
| 3 |
| 4 |
设AC=4k，BC=3k，
∵AC2+BC2=AB2，AB=10，
∴（4k）2+（3k）2=100．
∴k1=2，k2=-2（舍去）．
∴AC=8，BC=6．
过点D作DF⊥AB于F，
∵AD是∠CAB的角平分线，
∴CD=DF．
∵∠DFB=∠ACB=90°，∠DBF=∠ABC，
∴△DBF∽△ABC．
∴
| DB |
| AB |
| DF |
| AC |
即
| 6-CD |
| 10 |
| CD |
| 8 |
∴CD=
| 8 |
| 3 |
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
