题目内容
 如图,为了确定一条河的宽度AB,可以在点B一侧的岸边选择一点C,使得CB⊥AB,并量得CB=40米,测得∠ACB=45°,那么河的宽度AB是
如图,为了确定一条河的宽度AB,可以在点B一侧的岸边选择一点C,使得CB⊥AB,并量得CB=40米,测得∠ACB=45°,那么河的宽度AB是
- A.40米
- B.40
 米
米 - C.20米
- D.20
 米
米
A
分析:首先根据CB⊥AB得到直角三角形,然后根据∠ACB=45°得到等腰直角三角形,然后利用等腰直角三角形的两直角边相等即可得到答案.
解答:∵CB⊥AB,
∴∠B=90°,
∵∠ACB=45°,
∴∠A=∠ACB=45°,
∴AB=CB=40.
故选A.
点评:本题考查了等腰直角三角形的性质,解题的关键是根据题目提供的一些条件得到等腰直角三角形.
分析:首先根据CB⊥AB得到直角三角形,然后根据∠ACB=45°得到等腰直角三角形,然后利用等腰直角三角形的两直角边相等即可得到答案.
解答:∵CB⊥AB,
∴∠B=90°,
∵∠ACB=45°,
∴∠A=∠ACB=45°,
∴AB=CB=40.
故选A.
点评:本题考查了等腰直角三角形的性质,解题的关键是根据题目提供的一些条件得到等腰直角三角形.

练习册系列答案
相关题目
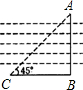 (2004•包头)如图,为了确定一条河的宽度AB,可以在点B一侧的岸边选择一点C,使得CB⊥AB,并量得CB=40米,测得∠ACB=45°,那么河的宽度AB是( )
(2004•包头)如图,为了确定一条河的宽度AB,可以在点B一侧的岸边选择一点C,使得CB⊥AB,并量得CB=40米,测得∠ACB=45°,那么河的宽度AB是( )

 米
米 米
米
 m
m m
m