ЬтФПФкШн
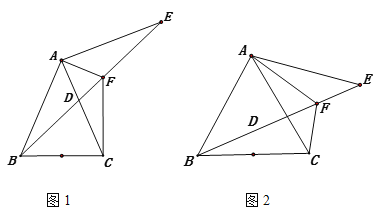
ЁОЬтФПЁПФГжабЇЦпФъМЖЭЌбЇЕНвАЭтПЊеЙЪ§бЇзлКЯЪЕМљЛюЖЏЃЌдкгЊЕиПДЕНвЛГиЬСЃЌЭЌбЇУЧЯыжЊЕРГиЬССНЖЫЕФОрРы.гавЛЮЛЭЌбЇЩшМЦСЫШчЯТВтСПЗНАИЃКЯШдкЦНЕиЩЯШЁвЛИіПЩжБНгЕНДяAЁЂBЕФЕуE(AЁЂBЮЊГиЬСЕФСНЖЫ)ЃЌСЌНгAEЁЂBEВЂЗжБ№бгГЄAEжСDЃЌBEжСCЃЌЪЙED=AE,EC=EBЃЌВтГіCDЕФГЄзїЮЊABжЎМфЕФОрРы.
(1)ЫћЕФЗНАИПЩааТ№?ЧыЫЕУїРэгЩ.
(2)ШєВтЕУCD=10mЃЌдђГиЬССНЖЫЕФОрРыЪЧЖрЩй?

ЁОД№АИЁПЃЈ1ЃЉИУЗНАИПЩааЃЛРэгЩМћНтЮіЃЛЃЈ2ЃЉ10
ЁОНтЮіЁП
ЃЈ1ЃЉетжжЩшМЦЗНАИРћгУСЫЁАБпНЧБпЁБХаЖЯСНИіШ§НЧаЮШЋЕШЃЌРћгУЖдгІБпЯрЕШЃЌЕУAB=CDЃЎЗНАИЕФВйзїадЧПЃЌашвЊВтСПЕФЯпЖЮКЭНЧЖШдкТНЕивЛВрМДПЩЪЕЪЉЃЛ
ЃЈ2ЃЉРћгУШЋЕШШ§НЧаЮЕФаджЪМДПЩЕУ.
ЃЈ1ЃЉПЩааЃЌРэгЩШчЯТЃК
дкЁїAEBКЭЁїDECжа

ЁрЁїAEBЁеЁїDECЃЈSASЃЉЃЛ
ЁрAB=CDЃЈШЋЕШШ§НЧаЮЕФЖдгІБпЯрЕШЃЉЃЎ
ЃЈ2ЃЉВтЕУCD=10mЃЌдђГиЬССНЖЫЕФОрРыAB=10mЃЌ
Д№ЃКГиЬССНЖЫЕФОрРыЪЧ10УзЃЎ

СЗЯАВсЯЕСаД№АИ
ЯрЙиЬтФП