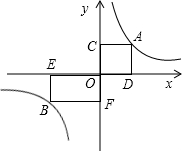
题目内容
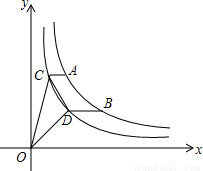
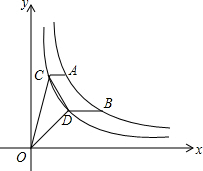 如图,A,B是函数
如图,A,B是函数 在第一象限图象上的两个点,C,D是函数
在第一象限图象上的两个点,C,D是函数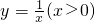 上两点,AC∥BD∥x轴,若
上两点,AC∥BD∥x轴,若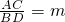 ,则△COD的面积是________(用含m的代数式表示).
,则△COD的面积是________(用含m的代数式表示).

分析:先根据反比例函数图象上点的坐标特征可设C(a,
 ),D(b,
),D(b, ),再由A,B是函数
),再由A,B是函数 在第一象限图象上的两个点,AC∥BD∥x轴,得出A(ak,
在第一象限图象上的两个点,AC∥BD∥x轴,得出A(ak, ),B(bk,
),B(bk, ),那么根据
),那么根据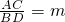 ,得出a=bm.过点C作CM⊥y轴于点M,作CN⊥x轴于点N,过点D作DP⊥x轴于点P,则△COD的面积=矩形ONCM的面积+梯形PDCN的面积-△COM的面积-△DOP的面积,由反比例函数系数k的几何意义,可知矩形ONCM的面积=1,△COM的面积=△DOP的面积=
,得出a=bm.过点C作CM⊥y轴于点M,作CN⊥x轴于点N,过点D作DP⊥x轴于点P,则△COD的面积=矩形ONCM的面积+梯形PDCN的面积-△COM的面积-△DOP的面积,由反比例函数系数k的几何意义,可知矩形ONCM的面积=1,△COM的面积=△DOP的面积= ,所以△COD的面积=梯形PDCN的面积,根据梯形的面积公式即可求解.
,所以△COD的面积=梯形PDCN的面积,根据梯形的面积公式即可求解.解答:
 解:∵C,D是函数
解:∵C,D是函数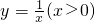 上两点,
上两点,∴可设C(a,
 ),D(b,
),D(b, ),
),∵A,B是函数
 在第一象限图象上的两个点,AC∥BD∥x轴,
在第一象限图象上的两个点,AC∥BD∥x轴,∴A(ak,
 ),B(bk,
),B(bk, ).
).∵
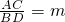 ,
,∴
 =m,
=m,由图可知k≠1,
∴a=bm.
如图,过点C作CM⊥y轴于点M,作CN⊥x轴于点N,过点D作DP⊥x轴于点P,
则△COD的面积=矩形ONCM的面积+梯形PDCN的面积-△COM的面积-△DOP的面积
=1+
 (
( +
+ )•(b-a)-
)•(b-a)- -
-
=
 (
( +
+ )•(b-bm)
)•(b-bm)=
 .
.故答案为
 .
.点评:本题考查了反比例函数图象上点的坐标特征,平行于坐标轴的直线上点的坐标特征,反比例函数系数k的几何意义,三角形的面积,有一定难度.运用数形结合的思想,准确地设出点的坐标是解题的关键.

练习册系列答案
相关题目
 如图,A、B是函数
如图,A、B是函数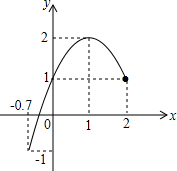 (2012•盐城模拟)已知二次函数的图象(-0.7≤x≤2)如图所示、关于该函数在所给自变量x的取值范围内,下列说法正确的是( )
(2012•盐城模拟)已知二次函数的图象(-0.7≤x≤2)如图所示、关于该函数在所给自变量x的取值范围内,下列说法正确的是( ) (2013•成都一模)如图,A,B是函数
(2013•成都一模)如图,A,B是函数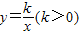 在第一象限图象上的两个点,C,D是函数
在第一象限图象上的两个点,C,D是函数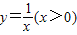 上两点,AC∥BD∥x轴,若
上两点,AC∥BD∥x轴,若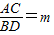 ,则△COD的面积是 (用含m的代数式表示).
,则△COD的面积是 (用含m的代数式表示).