题目内容
如图，直线MN是等腰直角三角形ABC的对称轴，斜边BC=10cm，以点A为圆心作半径为2cm的圆，若把⊙A沿MN向下平移，使⊙A与BC相切，则平移的距离为（ ）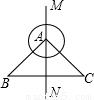
A．3cm
B．7cm
C．3cm或7cm
D．3cm或6cm
【答案】分析：根据等腰直角三角形性质求出BD=DC=5cm，求出AD=BD=5cm，分为两种情况：如图，即可求出平移的距离．
解答：
解：∵△BAC是等腰直角三角形，直线MN是等腰直角三角形ABC的对称轴，斜边BC=10cm，
∴∠B=45°，BD=CD=5cm，∠ADB=90°，
∴∠BAD=45°=∠B，
∴AD=BD=5cm，
∵以点A为圆心作半径为2cm的圆，若把⊙A沿MN向下平移，使⊙A与BC相切，
∴平移的距离为5cm-2cm=3cm或5cm+2cm=7cm，如图，
故选C．
点评：本题考查了等腰直角三角形性质，平移的性质，切线的性质，关键是求出符合条件的两种情况，题目比较好，但是比较容易出错．
解答：
解：∵△BAC是等腰直角三角形，直线MN是等腰直角三角形ABC的对称轴，斜边BC=10cm，∴∠B=45°，BD=CD=5cm，∠ADB=90°，
∴∠BAD=45°=∠B，
∴AD=BD=5cm，
∵以点A为圆心作半径为2cm的圆，若把⊙A沿MN向下平移，使⊙A与BC相切，
∴平移的距离为5cm-2cm=3cm或5cm+2cm=7cm，如图，
故选C．
点评：本题考查了等腰直角三角形性质，平移的性质，切线的性质，关键是求出符合条件的两种情况，题目比较好，但是比较容易出错．
练习册系列答案
相关题目
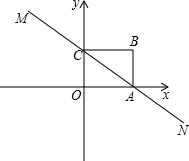（2013•绥化）如图，直线MN与x轴，y轴分别相交于A，C两点，分别过A，C两点作x轴，y轴的垂线相交于B点，且OA，OC（OA＞OC）的长分别是一元二次方程x2-14x+48=0的两个实数根．
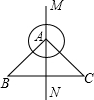如图，直线MN是等腰直角三角形ABC的对称轴，斜边BC=10cm，以点A为圆心作半径为2cm的圆，若把⊙A沿MN向下平移，使⊙A与BC相切，则平移的距离为（ ）
如图，直线MN与x轴，y轴分别相交于A，C两点，分别过A，C两点作x轴，y轴的垂线相交于B点，且OA，OC（OA＞OC）的长分别是一元二次方程x2-14x+48=0的两个实数根．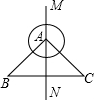
如图，直线MN是等腰直角三角形ABC的对称轴，斜边BC=10cm，以点A为圆心作半径为2cm的圆，若把⊙A沿MN向下平移，使⊙A与BC相切，则平移的距离为