题目内容
我们给出如下定义：若一个四边形中存在相邻两边的平方和等于一条对角线的平方，则称这个四边形为勾股四边形，这两条相邻的边称为这个四边形的勾股边．
（1）写出你所学过的特殊四边形中是勾股四边形的两种图形的名称_________，________；
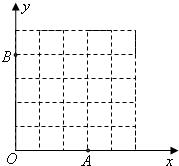
（2）如图，已知格点（小正方形的顶点）
，
，
，请你写出所有以格点为顶点，
为勾股边且对角线相等的勾股四边形
的顶点M的坐标；
（3）如图，将
绕顶点
按顺时针方向旋转
，得到
，连结
，
．求证：
，即四边形
是勾股四边形．
 |
解：
(1).长方形 .,正方形.
(2). M1(3, 4) M2(4, 3)
(3).证明:;连结EC
∵ABC≌DBE
∴BC=BE AC=DE
又∵∠CBE=600
∴CBE是等边三角形
∴∠BCE=600 BC=EC
又∵∠DCB=300
∴∠BCE+∠DCB=900
即∠DCE=900 .
DC2+EC2=AC2
练习册系列答案
相关题目
24、我们给出如下定义：若一个四边形中存在相邻两边的平方和等于一条对角线的平方，则称这个四边形为勾股四边形，这两条相邻的边称为这个四边形的勾股边．