题目内容
6.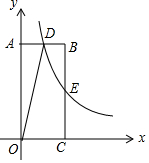 如图,在平面直角坐标系中,矩形OABC的顶点A在y轴正半轴上,点C在x轴正半轴上,函数y=$\frac{k}{x}$(x>0)的图象经过边BC的中点E,交AB于点D.若四边形ODBC的面积为6,则k的值为( )
如图,在平面直角坐标系中,矩形OABC的顶点A在y轴正半轴上,点C在x轴正半轴上,函数y=$\frac{k}{x}$(x>0)的图象经过边BC的中点E,交AB于点D.若四边形ODBC的面积为6,则k的值为( )| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
分析 连接OB、OE,由矩形的性质和已知条件得出△OBD的面积=△OBE的面积=△OCE的面积=$\frac{1}{3}$四边形ODBC的面积,即可求出△OCE的面积,即可得出k的值.
解答  解:连接OB、OE,如图所示:
解:连接OB、OE,如图所示:
∵四边形OABC是矩形,
∴∠OAD=∠OCE=∠DBE=90°,△OAB的面积=△OBC的面积,
∵D、E在反比例函数y=$\frac{k}{x}$(x>0)的图象上,
∴△OAD的面积=△OCE的面积,
∴△OBD的面积=△OBE的面积,
∵BE=EC,
∴△OCE的面积=△OBE的面积
∵△OCE的面积=$\frac{1}{3}$四边形ODBC的面积=2,
∴k=4.
故选C.
点评 本题考查了反比例函数的系数k的几何意义,在反比例函数y=xk图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|k|,且保持不变.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
10.从$\sqrt{2}$,0,π,3.14,6这5个数中随机抽取一个数,抽到有理数的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
8.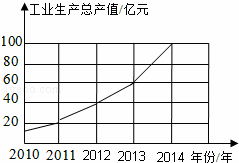 如图,是根据某市2010年至2014年工业生产总值绘制的折线统计图,观察统计图获得以下信息,其中信息判断错误的是( )
如图,是根据某市2010年至2014年工业生产总值绘制的折线统计图,观察统计图获得以下信息,其中信息判断错误的是( )
 如图,是根据某市2010年至2014年工业生产总值绘制的折线统计图,观察统计图获得以下信息,其中信息判断错误的是( )
如图,是根据某市2010年至2014年工业生产总值绘制的折线统计图,观察统计图获得以下信息,其中信息判断错误的是( )| A. | 2010年至2014年间工业生产总值逐年增加 | |
| B. | 2014年的工业生产总值比前一年增加了40亿元 | |
| C. | 2012年与2013年每一年与前一年比,其增长额相同 | |
| D. | 从2011年至2014年,每一年与前一年比,2014年的增长率最大 |
1.24的素因数是( )
| A. | 1,2,3,4,6,8,12,24 | B. | 2,3 | ||
| C. | 1,2,3 | D. | 2,2,2,3 |
11.正方体A的体积是正方体B的体积的27倍,那么正方体A的棱长是正方体B的棱长的( )
| A. | 2倍 | B. | 3倍 | C. | 4倍 | D. | 5倍 |
18.用四舍五入法得到近似数4.005万,关于这个数有下列说法,其中正确的是( )
| A. | 它精确到万位 | B. | 它精确到0.001 | C. | 它精确到万分位 | D. | 它精确到十位 |
15.在下列运算中,计算正确的是( )
| A. | m2+m2=m4 | B. | (m+1)2=m2+1 | C. | (3mn2)2=6m2n4 | D. | 2m2n÷(-mn)=-2m |
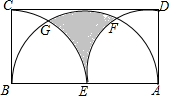 如图,矩形ABCD中,BC=4,以顶点A,B为圆心,以AD、BC长为半径作两条弧,两弧相切于点E,且E在AB上,以AB为直径作半圆恰好与DC相切,则图中阴影部分的面积为8$\sqrt{3}$-$\frac{8}{3}$π.
如图,矩形ABCD中,BC=4,以顶点A,B为圆心,以AD、BC长为半径作两条弧,两弧相切于点E,且E在AB上,以AB为直径作半圆恰好与DC相切,则图中阴影部分的面积为8$\sqrt{3}$-$\frac{8}{3}$π.