��Ŀ����
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬CA=8��CB=6������P��C������CA������ÿ��1����λ���ȵ��ٶ���A�������˶�������A���������ԭ���ٶ���AC���أ�ͬʱ����Q�ӵ�A������AB��ÿ��1����λ�������B�����˶�����Q����Bʱ��P��Q����ͬʱֹͣ�˶�����P��Q�˶���ʱ��Ϊt�루t��0����
��1����tΪ��ֵʱ��PQ��CB��
��2���ڵ�P��C��A�˶��Ĺ����У���CB���Ƿ���ڵ�Eʹ��CEP����PQAȫ�ȣ������ڣ����CE�ij����������ڣ���˵�����ɣ�
��3��������P��Q������˶����߶�PQ�Ĵ�ֱƽ����DF��PQ�ڵ�D��������QB��BC��CP�ڵ�F����DF������Cʱ�����t��ֵ��

���𰸡���1��![]() ����2�����ڣ�
����2�����ڣ�![]() ����3��5��10.
����3��5��10.
�������������������1�����ݹ��ɶ������AB������ƽ���߷��߶γɱ��������г�����ʽ�����㼴�ɣ�
��2������ȫ�������ε����ʵõ���PQA=90�㣬�������������ε��������PE�����ݹ��ɶ������㣻
��3����P��C��A�˶���P��A��C�˶���������������߶δ�ֱƽ���ߵ����ʡ����������ε����ʼ��㣮
�⣺��1����ͼ1��
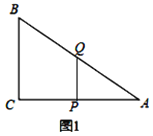
CP=AQ=t����AP=8��t����Rt��ABC�У��ɹ��ɶ����ɵ�AB=10��
��PQ��CB�ɵ�![]() ����
����![]() ��
��
���t=![]() �����Ե�t=
�����Ե�t=![]() ʱ��PQ��CB .
ʱ��PQ��CB .
��2�����ڣ���ͼ2��
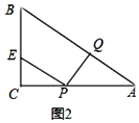
�������֪CP=AQ=t���֡ߡ�PCE =90����Ҫʹ��CEP����PQAȫ�ȣ�
ֻ�С�PQA=90�㣬
��һ���������ʱCE=PQ��PE= AP������PQA�ס�BCA�ɵ�![]() ��
��
��![]() �����t=
�����t=![]() ��
��
��PE=8��t=![]() ����Rt��PCE�У��ɹ��ɶ����ɵ�CE=
����Rt��PCE�У��ɹ��ɶ����ɵ�CE=![]() ��
��
(������PCE�ס�ACB��![]() ����
����![]() �����CE=
�����CE=![]() ��
��
��3���ٵ�P��C��A�˶�ʱ��CQ=CP=AQ=t���ɵá�QCA=��QAC��
���ԡ�QCB=��QBC������CQ=BQ=t������BQ=AQ=![]() AB��
AB��
��AB=2t�����t=5��
����ͼ3��
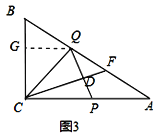
��P��A��C�˶�ʱ����Q��QG��CB��CB�ڵ�G��
CQ=CP=16��t��BQ=10��t����![]() ����
����![]() ������GQ=
������GQ=![]() ��10��t����
��10��t����
ͬ�������BG=![]() ��10��t��������GC=6��
��10��t��������GC=6��![]() ��10��t����
��10��t����
��Rt��CGQ�У��ɹ��ɶ����ɵã�CG2+GQ2=CQ2��
��[6��![]() ��10��t��]2+[
��10��t��]2+[![]() ��10��t��]2=��16��t��2�����t=10.
��10��t��]2=��16��t��2�����t=10.
���Ͽ�֪����������t��ֵΪ5��10��

 ��У����ϵ�д�
��У����ϵ�д�