题目内容
如图，每个多边形的边长都大于2，分别以多边形的各顶点为圆心，1为半径画弧（弧的端点分别在多边形的相邻两边上），则第6个图形中所有弧的弧长的和是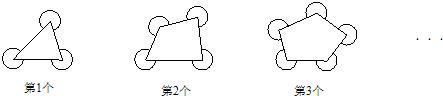
分析：根据弧长公式计算所给三个图形的弧长和，从中发现规律进一步推广即可．
解答：解：根据弧长公式可得第一个图形中的所有弧长的圆心角的和=360×3-180=180×5度．
则弧长和=
=5π，
依此算第二个图形的弧长和=6π，
推而广之：第n个图形的弧长和是5π+（n-1）π=（n+4）π，
∴第6个图形中所有弧的弧长的和是10π．
则弧长和=
| 180×5π×1 |
| 180 |
依此算第二个图形的弧长和=6π，
推而广之：第n个图形的弧长和是5π+（n-1）π=（n+4）π，
∴第6个图形中所有弧的弧长的和是10π．
点评：此题的重点是计算所有弧长的圆心角的和．
练习册系列答案
相关题目
24、同学们，你们会用画多边形的对角线来解决生活中的数学问题吗？
