题目内容
已知在△ABC中,AB=AC=9,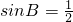 ,把△ABC绕点A旋转,使得边AB落在边AC上,此时点C落在点D的位置上,那么点D与旋转前点B之间的距离等于________.
,把△ABC绕点A旋转,使得边AB落在边AC上,此时点C落在点D的位置上,那么点D与旋转前点B之间的距离等于________.
9
分析:根据锐角三角函数值求出∠B=30°,再根据等腰三角形两底角相等,利用三角形内角和等于180°求出∠BAC=120°,根据旋转的性质可得∠CAD=120°,AD=AC,然后根据周角等于360°求出∠BAD=120°,从而求出BD=BC,再解直角三角形求出BC的长度,即可得解.
解答: 解:如图,∵sinB=
解:如图,∵sinB= ,
,
∴∠ABC=30°,
∵AB=AC,
∴∠ABC=∠ACB=30°,
∴∠BAC=180°-30°-30°=120°,
又∵△ACD是△ABC旋转得到,
∴∠CAD=120°,AD=AC,
∴∠BAD=360°-120°-120°=120°,
∴点D到点B的距离BD=BC,
在△ABC中,BC=2AB•cos30°=2×9× =9
=9 ,
,
所以BD=9 .
.
故答案为:9 .
.
点评:本题考查了旋转的性质,特殊角的三角函数值,根据题目数据求出∠BAC、∠CAD、∠BAD都是120°角是解题的关键.

分析:根据锐角三角函数值求出∠B=30°,再根据等腰三角形两底角相等,利用三角形内角和等于180°求出∠BAC=120°,根据旋转的性质可得∠CAD=120°,AD=AC,然后根据周角等于360°求出∠BAD=120°,从而求出BD=BC,再解直角三角形求出BC的长度,即可得解.
解答:
 解:如图,∵sinB=
解:如图,∵sinB= ,
,∴∠ABC=30°,
∵AB=AC,
∴∠ABC=∠ACB=30°,
∴∠BAC=180°-30°-30°=120°,
又∵△ACD是△ABC旋转得到,
∴∠CAD=120°,AD=AC,
∴∠BAD=360°-120°-120°=120°,
∴点D到点B的距离BD=BC,
在△ABC中,BC=2AB•cos30°=2×9×
 =9
=9 ,
,所以BD=9
 .
.故答案为:9
 .
.点评:本题考查了旋转的性质,特殊角的三角函数值,根据题目数据求出∠BAC、∠CAD、∠BAD都是120°角是解题的关键.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 22、如图,已知在△ABC中,∠A=(2x+10)°,∠B=(3x)°,∠ACD是△ABC的一个外角,且∠ACD=(6x-10)°,求∠A的度数.
22、如图,已知在△ABC中,∠A=(2x+10)°,∠B=(3x)°,∠ACD是△ABC的一个外角,且∠ACD=(6x-10)°,求∠A的度数.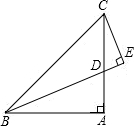 如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E.若BD平分∠ABC.
如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E.若BD平分∠ABC. 如图,已知在△ABC中,∠B与∠C的平分线交于点P.
如图,已知在△ABC中,∠B与∠C的平分线交于点P.