题目内容
如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆恰好与BC相切于点D,分别交AC、AB于点E、F.
(1)若∠B=30°,求证:以A、O、D、E为顶点的四边形是菱形.
(2)若AC=6,AB=10,连结AD,求⊙O的半径和AD的长.

(1)证明:如图1,连接OD、OE、ED.
∵BC与⊙O相切于一点D,
∴OD⊥BC,
∴∠ODB=90°=∠C,
∴OD∥AC,
∵∠B=30°,
∴∠A=60°,
∵OA=OE,
∴△AOE是等边三角形,
∴AE=AO=0D,
∴四边形AODE是平行四边形,
∵OA=OD,
∴四边形AODE是菱形.
(2)解:设⊙O的半径为r.
∵OD∥AC,
∴△OBD∽△ABC.
∴ ,即8r=6(8﹣r).
,即8r=6(8﹣r).
解得r= ,
,
∴⊙O的半径为 .
.
如图2,连接OD、DF.
∵OD∥AC,
∴∠DAC=∠ADO,
∵OA=OD,
∴∠ADO=∠DAO,
∴∠DAC=∠DAO,
∵AF是⊙O的直径,
∴∠ADF=90°=∠C,
∴△ADC∽△AFD,
∴ ,
,
∴AD2=AC•AF,
∵AC=6,AF= ,
,
∴AD2= ×6=45,
×6=45,
∴AD= =3
=3 .
.



练习册系列答案
相关题目
如图,AB∥CD,∠A=50°,则∠1的大小是( )

|
| A. | 50° | B. | 120° | C. | 130° | D. | 150° |
在直角坐标系中,将点(﹣2,3)关于原点的对称点向左平移2个单位长度得到的点的坐标是( )
|
| A. | (4,﹣3) | B. | (﹣4,3) | C. | (0,﹣3) | D. | (0,3) |
 名学生中,随机抽取部分学生进行问卷调查(每名学生只能填写一项自己喜欢的活动项目),并将调查结果绘制成如下两幅不完整的统计图.
名学生中,随机抽取部分学生进行问卷调查(每名学生只能填写一项自己喜欢的活动项目),并将调查结果绘制成如下两幅不完整的统计图.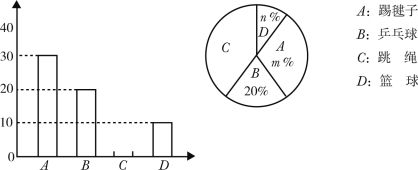
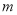 = ,
= ,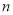 = ,表示区域
= ,表示区域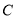 的圆心角为 °;
的圆心角为 °; .其中
.其中 满足一元二次方程
满足一元二次方程 .
. |+
|+ +(﹣2)0;
+(﹣2)0;

 +
+ .
.