Question

根据三视图（课本134页第8题），求它们表示的几何体的体积（图中标有尺寸）．

Answer 1

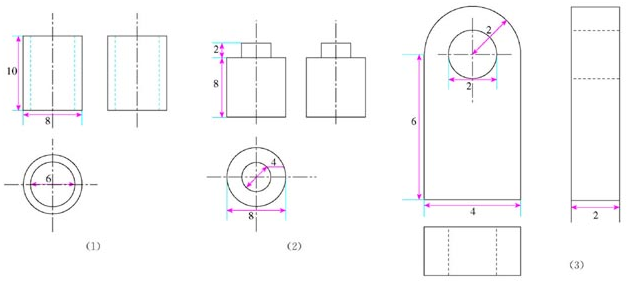
分析：（1）利用三视图可以得出此物体是空心圆柱，进而利用圆柱体体积求法得出答案即可；
（2）根据三视图可以得出此物体是两圆柱叠放，进而利用圆柱体体积求法得出答案即可；
（3）根据三视图可以得出此物体是一个长方体和半圆柱以及半圆柱和长方体交界是圆柱形空的组合体，进而利用圆柱体体积求法以及长方体体积求法得出答案即可．

解答：解：（1）根据三视图可以得出此物体是空心圆柱，
其体积为：V=[π×（

8

2

）²-π×（

6

2

）²]×10=70π；

（2）根据三视图可以得出此物体是两圆柱叠放，
其体积为：V=π×（

8

2

）²×8+π×（

4

2

）²×2=136π；

（3）根据三视图可以得出此物体是一个长方体和半圆柱以及半圆柱和长方体交界是圆柱形空的组合体，
其体积为：V=4×6×2+

1

2

π×（

4

2

）²×2-π×（

2

2

）²×2=48+2π．

点评：此题主要考查了由三视图判断几何体以及圆柱体体积求法和长方体体积求法，正确判断出几何体的形状是解题关键．