题目内容
如图，一段抛物线：y＝－x(x－3)（0≤x≤3），记为C1，它与x轴交于点O，A1；将C1绕点A1旋转180°得C2，交x 轴于点A2；将C2绕点A2旋转180°得C3，交x 轴于点A3；……如此进行下去，直至得C13．若P（37，m）在第13段抛物线C13上，则m =_________．
【答案】
2
【解析】
试题分析：∵一段抛物线：
（
），
∴图象与x轴交点坐标为：（0，0），（3，0），
∵将
绕点
旋转180°得
，交x轴于点
；
将绕点旋转180°得
，交x轴于点
；
…
如此进行下去，直至得
．
∴的与x轴的交点横坐标为（36，0），（39，0），且图象在x轴上方，
∴的解析式为：
=-（x-36）（x-39），
当x=37时，y=-（37-36）×（37-39）=2．
考点：二次函数的性质
练习册系列答案
名校课堂系列答案
相关题目
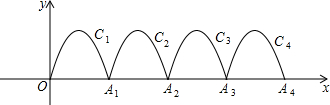
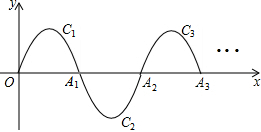（2013•河北）如图，一段抛物线：y=-x（x-3）（0≤x≤3），记为C1，它与x轴交于点O，A1；
（0≤x≤3），记为C1，它与x轴交于点O，A1；
