题目内容
已知:抛物线y=ax2+bx+c过点A(一1,4),其顶点的横坐标为| 1 |
| 2 |
(1)求此抛物线的解析式及顶点E的坐标;
(2)设此抛物线与y轴交于D点,点P是抛物线上的点,若△PBO的面积为△DOC面积的
| 2 |
| 3 |
分析:(1)首先认真阅读题目要求,画出如下图所示,根据抛物线y=ax2+bx+c过点A(-1,4)列出关系式4=a-b+c;根据抛物线y=ax2+bx+c顶点的横坐标为
列出关系式-
=
;与x轴分别交于B(x1,0)、C(x2,0)两点(其中且x1<x2),且x12+x22=13,那么可得到方程ax2+bx+c=0,因此x1+x2=-
,x1•x2=
,则利用完全平方式可得
-2×
=13.联立三式组成方程组,可解得a、b、c的值,则抛物线的解析式即可确定.再将解析式写出顶点式,则顶点坐标E也就确定.
(2)设P的坐标为(m、n).首先结合图形,求得B、C、D点的坐标.再用n表示出△PBO的面积,并求得△DOC面积的面积,根据两个三角形的面积比,求得n的取值,则m的取值,也就可求出.
| 1 |
| 2 |
| b |
| 2a |
| 1 |
| 2 |
| b |
| a |
| c |
| a |
| b2 |
| a2 |
| c |
| a |
(2)设P的坐标为(m、n).首先结合图形,求得B、C、D点的坐标.再用n表示出△PBO的面积,并求得△DOC面积的面积,根据两个三角形的面积比,求得n的取值,则m的取值,也就可求出.
解答:解:(1)由题意得
?
?
将①②代入②得 a=-1,则b=1,c=6
∴该抛物线的解析式为y=-x2+x+6= -(x-
-(x-
)2+
∴顶点E的坐标为(
,
)
(2)抛物线与y轴交点D的横坐标为x=0,则y=6,即D(0,6)
∵-x2+x+6=0?-(x-3)(x+2)=0,即x=-2或3
∴B(-2,0)、C(3,0)
设P的坐标为(m、n)
S△BOP=
×2×|n|
S△DOC=
×3×6=9
又∵S△BOP=
S△DOC,即
×2×|n|=
×9
∴n=6或-6
当n=6时,则6=-m2+m+6,解得m=0或1;
当n=-6时,则-6=-m2+m+6,解得m=-3或4.
∴点P的坐标为(0,6)、(-1,6)、(-3,-6)、(4,-6)
答:(1)该抛物线的解析式为y=-x2+x+6,顶点E的纵坐标为(
,
);
(2)点P的坐标为(0,6)、(-1,6)、(-3,-6)、(4,-6).
|
|
|
将①②代入②得 a=-1,则b=1,c=6
∴该抛物线的解析式为y=-x2+x+6=
 -(x-
-(x-| 1 |
| 2 |
| 25 |
| 4 |
∴顶点E的坐标为(
| 1 |
| 2 |
| 25 |
| 4 |
(2)抛物线与y轴交点D的横坐标为x=0,则y=6,即D(0,6)
∵-x2+x+6=0?-(x-3)(x+2)=0,即x=-2或3
∴B(-2,0)、C(3,0)
设P的坐标为(m、n)
S△BOP=
| 1 |
| 2 |
S△DOC=
| 1 |
| 2 |
又∵S△BOP=
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
∴n=6或-6
当n=6时,则6=-m2+m+6,解得m=0或1;
当n=-6时,则-6=-m2+m+6,解得m=-3或4.
∴点P的坐标为(0,6)、(-1,6)、(-3,-6)、(4,-6)
答:(1)该抛物线的解析式为y=-x2+x+6,顶点E的纵坐标为(
| 1 |
| 2 |
| 25 |
| 4 |
(2)点P的坐标为(0,6)、(-1,6)、(-3,-6)、(4,-6).
点评:本题是二次函数的综合题型,其中涉及到的知识点有抛物线的顶点公式和三角形的面积求法.在求有关动点问题时要注意分析题意分情况讨论结果.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
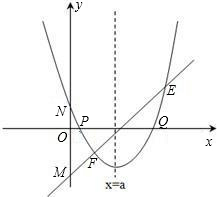 存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由. (2013•贵阳)已知:直线y=ax+b过抛物线y=-x2-2x+3的顶点P,如图所示.
(2013•贵阳)已知:直线y=ax+b过抛物线y=-x2-2x+3的顶点P,如图所示.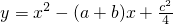 ,其中a、b、c是△ABC的∠A、∠B、∠C的对边.
,其中a、b、c是△ABC的∠A、∠B、∠C的对边. ,抛物线与x轴交于点P、Q,问是否
,抛物线与x轴交于点P、Q,问是否 存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由. ,其中a、b、c是△ABC的∠A、∠B、∠C的对边.
,其中a、b、c是△ABC的∠A、∠B、∠C的对边.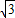 ,抛物线与x轴交于点P、Q,问是否存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
,抛物线与x轴交于点P、Q,问是否存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.