题目内容
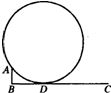 10、设计一把直尺ABC,BC在地面上,AB与地面垂直,并且AB=10cm,移动一个半径不小于10cm的圆形轮子,使轮子紧靠A点,且与BC相切于D点(如图).设计要求在D处的刻度恰好显示这个轮子的半径(以厘米为单位).那么,当BC的长度为1M时,BC上可标出的最大刻度是
10、设计一把直尺ABC,BC在地面上,AB与地面垂直,并且AB=10cm,移动一个半径不小于10cm的圆形轮子,使轮子紧靠A点,且与BC相切于D点(如图).设计要求在D处的刻度恰好显示这个轮子的半径(以厘米为单位).那么,当BC的长度为1M时,BC上可标出的最大刻度是
505
.分析:连接OA、OC,过A做AH⊥OC于H,构造直角三角形OAH,设OA=OD=r,根据勾股定理即可求出半径.
解答: 解:AB=10,BC=100,
解:AB=10,BC=100,
连接OA、OC,过A做AH⊥OC于H,
设OA=OD=r,
当D与C重合时,半径r为最大,
就是标出的最大刻度,
此时OH=r-10,AH=BC=100,
由勾股定理得:1002+(r-10)2=r2,
解得:r=505.
 解:AB=10,BC=100,
解:AB=10,BC=100,连接OA、OC,过A做AH⊥OC于H,
设OA=OD=r,
当D与C重合时,半径r为最大,
就是标出的最大刻度,
此时OH=r-10,AH=BC=100,
由勾股定理得:1002+(r-10)2=r2,
解得:r=505.
点评:本题主要考查了切线的性质,勾股定理等知识点,解此题的关键是理解题意和构造直角三角形.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
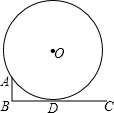 设计一把直尺ABC,BC在地面上,AB与地面垂直,并且AB=10cm,移动一个半径不小于10cm的圆形轮子,使轮子紧靠A点,且与BC相切于D点(如图).设计要求在D处的刻度恰好显示这个轮子的半径(以厘米为单位).那么,当BC的长度为1M时,BC上可标出的最大刻度是________.
设计一把直尺ABC,BC在地面上,AB与地面垂直,并且AB=10cm,移动一个半径不小于10cm的圆形轮子,使轮子紧靠A点,且与BC相切于D点(如图).设计要求在D处的刻度恰好显示这个轮子的半径(以厘米为单位).那么,当BC的长度为1M时,BC上可标出的最大刻度是________.