题目内容
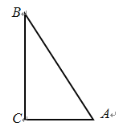
【题目】如图,![]() 中,
中,![]() ,
,![]() ,面积为150.
,面积为150.
(1)尺规作图:作![]() 的平分线交
的平分线交![]() 于点
于点![]() ;(不要求写作法,保留作图痕迹)
;(不要求写作法,保留作图痕迹)
(2)在(1)的条件下,求出点![]() 到两条直角边的距离.
到两条直角边的距离.
【答案】(1)见解析;(2)![]()
【解析】
(1)利用尺规作图的步骤作出∠ACB的平分线交AB于点D即可;
(2)作![]() 于E,
于E,![]() 于F,根据面积求出BC的长.法一:根据角平分线的性质得出DE=DF,从而得出四边形CEDF为正方形.再由
于F,根据面积求出BC的长.法一:根据角平分线的性质得出DE=DF,从而得出四边形CEDF为正方形.再由![]() ,得出
,得出![]() ,列方程可以求出结果;法二:根据
,列方程可以求出结果;法二:根据![]() ,利用面积法可求得DE,DF的值.
,利用面积法可求得DE,DF的值.
解:(1)∠ACB的平分线CD如图所示:

(2)已知![]() ,面积为150,∴
,面积为150,∴![]() .
.
法一:作![]() ,
,![]() ,
,

∵![]() 是
是![]() 角平分线,
角平分线,
∴![]() ,
,![]() ,而
,而![]() ,
,
∴四边形![]() 为正方形.
为正方形.
设![]() 为
为![]() ,则由
,则由![]() ,
,
∴![]() ,∴
,∴![]() .
.
即![]() ,得
,得![]() .
.
∴点![]() 到两条直角边的距离为
到两条直角边的距离为![]() .
.
法二:![]() ,
,
即![]() ,
,
又由(1)知AC=15,BC=20,
∴![]() ,
,
∴![]() .
.
故点![]() 到两条直角边的距离为
到两条直角边的距离为![]() .
.

【题目】空间任意选定一点![]() ,以点
,以点![]() 为端点,作三条互相垂直的射线
为端点,作三条互相垂直的射线![]() ,
,![]() ,
,![]() .这三条互相垂直的射线分别称作
.这三条互相垂直的射线分别称作![]() 轴、
轴、![]() 轴、
轴、![]() 轴,统称为坐标轴,它们的方向分别为
轴,统称为坐标轴,它们的方向分别为![]() (水平向前),
(水平向前),![]() (水平向右),
(水平向右),![]() (竖直向上)方向,这样的坐标系称为空间直角坐标系.将相邻三个面的面积记为
(竖直向上)方向,这样的坐标系称为空间直角坐标系.将相邻三个面的面积记为![]() ,
,![]() ,
,![]() ,且
,且![]() 的小长方体称为单位长方体,现将若干个单位长方体在空间直角坐标系内进行码放,要求码放时将单位长方体
的小长方体称为单位长方体,现将若干个单位长方体在空间直角坐标系内进行码放,要求码放时将单位长方体![]() 所在的面与
所在的面与![]() 轴垂直,
轴垂直,![]() 所在的面与
所在的面与![]() 轴垂直,
轴垂直,![]() 所在的面与
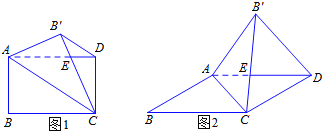
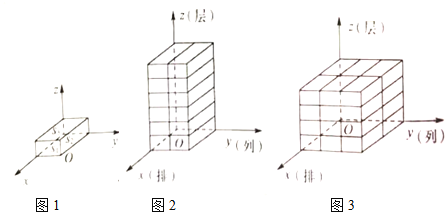
所在的面与![]() 轴垂直,如图1所示.若将
轴垂直,如图1所示.若将![]() 轴方向表示的量称为几何体码放的排数,
轴方向表示的量称为几何体码放的排数,![]() 轴方向表示的量称为几何体码放的列数,二轴方向表示的量称为几何体码放的层数;如图2是由若干个单位长方体在空间直角坐标内码放的一个几何体,其中这个几何体共码放了
轴方向表示的量称为几何体码放的列数,二轴方向表示的量称为几何体码放的层数;如图2是由若干个单位长方体在空间直角坐标内码放的一个几何体,其中这个几何体共码放了![]() 排
排![]() 列
列![]() 层,用有序数组记作
层,用有序数组记作![]() ,如图3的几何体码放了
,如图3的几何体码放了![]() 排
排![]() 列
列![]() 层,用有序数组记作
层,用有序数组记作![]() .这样我们就可用每一个有序数组
.这样我们就可用每一个有序数组![]() 表示一种几何体的码放方式.
表示一种几何体的码放方式.
(1)有序数组![]() 所对应的码放的几何体是______________;
所对应的码放的几何体是______________;
A.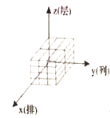 B.
B.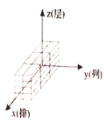 C.
C.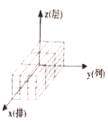 D.
D.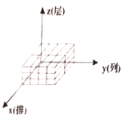
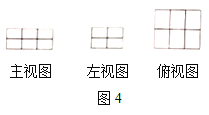
(2)图4是由若干个单位长方体码放的一个几何体的三视图,则这种码放方式的有序数组为(______,_______,_______),组成这个几何体的单位长方体的个数为____________个.
(3)为了进一步探究有序数组![]() 的几何体的表面积公式
的几何体的表面积公式![]() ,某同学针对若干个单位长方体进行码放,制作了下列表格:
,某同学针对若干个单位长方体进行码放,制作了下列表格:
几何体有序数组 | 单位长方体的个数 | 表面上面积为S1的个数 | 表面上面积为S2的个数 | 表面上面积为S3的个数 | 表面积 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
根据以上规律,请直接写出有序数组![]() 的几何体表面积
的几何体表面积![]() 的计算公式;(用
的计算公式;(用![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 表示)
表示)
(4)当![]() ,
,![]() ,
,![]() 时,对由
时,对由![]() 个单位长方体码放的几何体进行打包,为了节约外包装材料,我们可以对
个单位长方体码放的几何体进行打包,为了节约外包装材料,我们可以对![]() 个单位长方体码放的几何体表面积最小的规律进行探究,请你根据自己探究的结果直接写出使几何体表面积最小的有序数组,这个有序数组为(______,_______, ______),此时求出的这个几何体表面积的大小为____________(缝隙不计)
个单位长方体码放的几何体表面积最小的规律进行探究,请你根据自己探究的结果直接写出使几何体表面积最小的有序数组,这个有序数组为(______,_______, ______),此时求出的这个几何体表面积的大小为____________(缝隙不计)