Question

如图把△ABC纸片沿DE折叠，使点A落在四边形BCDE内部点A′的位置．如果∠A=40°，则∠1+∠2的度数为

1. A.
   40°
2. B.
   60°
3. C.
   80°
4. D.
   140°

Answer 1

C
分析：根据平角定义和折叠的性质，得∠1+∠2=360°-2（∠3+∠4），再利用三角形的内角和定理进行转换，得∠1+∠2=360°-2（180°-∠A）=2∠A．
解答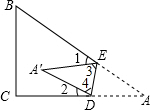：解：根据平角的定义和折叠的性质，得
∠1+∠2=360°-2（∠3+∠4）．
又∵∠3+∠4=180°-∠A，
∴∠1+∠2=360°-2（180°-∠A）=2∠A=80°．
故选C．
点评：此题综合运用了平角的定义、折叠的性质和三角形的内角和定理．