题目内容
按如图方式作正方形和等腰直角三角形．若第一个正方形的边长AB=1，第一个正方形与第一个等腰直角三角形的面积和为S1，第二个正方形与第二个等腰直角三角形的面积和为S2，…，则第n个正方形与第n个等腰直角三角形的面积和Sn= ．
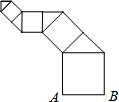
观察图形，根据正方形的四条边相等和等腰直角三角形的腰长为斜边长的
倍，分别求得每个正方形的边长，从而发现规律，再根据规律求出第n个正方形与第n个等腰直角三角形的面积和即可．
解：∵第一个正方形的边长为1，
第2个正方形的边长为（）1=，
第3个正方形的边长为（）2=
，
…，
第n个正方形的边长为（）n﹣1，
∴第n个正方形的面积为：[（）2]n﹣1=
，
则第n个等腰直角三角形的面积为：
×
=
，
故第n个正方形与第n个等腰直角三角形的面积和Sn=+=．
故答案为：．
倍，分别求得每个正方形的边长，从而发现规律，再根据规律求出第n个正方形与第n个等腰直角三角形的面积和即可．解：∵第一个正方形的边长为1，
第2个正方形的边长为（
）1=，第3个正方形的边长为（
）2=，…，
第n个正方形的边长为（
）n﹣1，∴第n个正方形的面积为：[（
）2]n﹣1=，则第n个等腰直角三角形的面积为：
×=，故第n个正方形与第n个等腰直角三角形的面积和Sn=
+=．故答案为：
．
练习册系列答案
相关题目
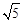.由此可知新正方形边长等于两个小正方形组成的矩形的对角线长．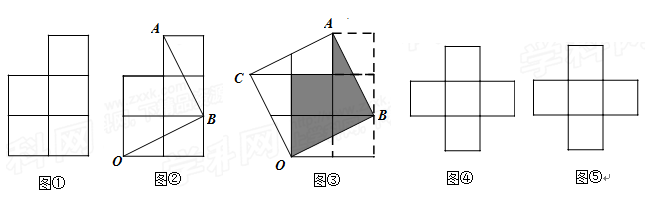
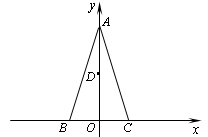
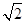)，C(1，0)， D为射线AO上一点，一动点P从A出发，运动路径为A→D→C，点P在AD上的运动速度是在CD上的3倍，要使整个运动时间最少，则点D的坐标应为（ ）
)
)
)
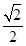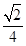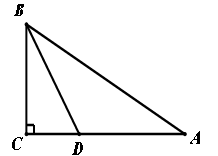
，腰长为
，则这个三角形的面积为 .