题目内容
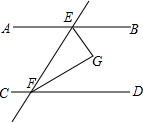 如图,直线AB∥CD,直线AB、CD被直线EF所截,EG平分∠BEF,FG平分∠DFE,试判断∠EFG的形状,并写出完整的说理过程.
如图,直线AB∥CD,直线AB、CD被直线EF所截,EG平分∠BEF,FG平分∠DFE,试判断∠EFG的形状,并写出完整的说理过程.
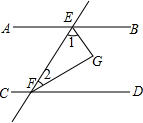 解:∵AB∥CD,∴∠BEF+∠DFE=180°,又∵EG平分∠BEF,FG平分∠DFE,
解:∵AB∥CD,∴∠BEF+∠DFE=180°,又∵EG平分∠BEF,FG平分∠DFE,∴∠1=
 ∠BEF,∠2=
∠BEF,∠2= ∠DFE,∴∠1+∠2=
∠DFE,∴∠1+∠2= (∠BEF+∠DFE)=
(∠BEF+∠DFE)= ×180°=90°,
×180°=90°,∴∠EGF=180°-(∠1+∠2)=180°-90°=90°.
∴△EFG是直角三角形.
分析:先根据AB∥CD求出∠BEF与∠DFE的关系,再由角平分线的性质求出∠1+∠2的度数,由三角形内角和定理即可求出∠EGF的度数,进而可得出答案.
点评:本题考查的是平行线的性质以及角平分线的性质和三角形内角和定理,比较简单.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 22、如图,直线AB∥CD,直线EF分别交直线AB、CD于点E、F,FH平分∠EFD,若∠FEH=110°,求∠EHF的度数.
22、如图,直线AB∥CD,直线EF分别交直线AB、CD于点E、F,FH平分∠EFD,若∠FEH=110°,求∠EHF的度数. 2、如图,直线AB∥CD,EF⊥AB于E,交CD于F,直线MN交AB于M,CD于N,EF于O,则直线AB和CD之间的距离是哪个线段的长( )
2、如图,直线AB∥CD,EF⊥AB于E,交CD于F,直线MN交AB于M,CD于N,EF于O,则直线AB和CD之间的距离是哪个线段的长( ) 9、如图,直线AB∥CD,∠A=45°,∠C=125°,则∠E=
9、如图,直线AB∥CD,∠A=45°,∠C=125°,则∠E=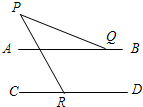 14、如图,直线AB∥CD,∠PQA=25°,∠PRC=60°,则∠P=
14、如图,直线AB∥CD,∠PQA=25°,∠PRC=60°,则∠P= (2012•高安市二模)如图,直线AB∥CD,GH与AB、CD分别交于点M、F,若∠GMB=70°,∠CEF=50°,则∠C=
(2012•高安市二模)如图,直线AB∥CD,GH与AB、CD分别交于点M、F,若∠GMB=70°,∠CEF=50°,则∠C=