题目内容
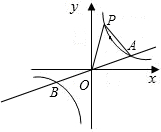 如图,正比例函数
如图,正比例函数 的图象与反比例函数
的图象与反比例函数 的图象交于A、B两点,点A的横坐标为6.
的图象交于A、B两点,点A的横坐标为6.
(1)求反比例函数的表达式;
(2)点P为此反比例函数图象上一点,且点P的纵坐标为4,求△AOP的面积.
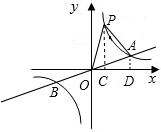 解:(1)∵点A的横坐标为6,
解:(1)∵点A的横坐标为6,∴纵坐标为
 ×6=2,
×6=2,∴k=2×6=12,
∴反比例函数的表达式为y=
 ;
;(2∵点P的纵坐标为4,
∴横坐标为3,
∴S△AOP=S△OPC+S梯形PCDA-S△AOD=S梯形PCDA=
 (2+4)×(6-3)=9.
(2+4)×(6-3)=9.分析:(1)易得点A的坐标,代入反比例函数解析式可得k的值;
(2)易得点P的坐标,作出PC,AD分别垂直于x轴,易得△AOP的面积为梯形PCDA的面积.
点评:考查一次函数与反比例函数相交的问题;得到所求三角形与所给点的坐标的关系是解决本题的关键.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
 如图,正比例函数
如图,正比例函数 OC的面积是24,且cos∠AOC=
OC的面积是24,且cos∠AOC= 已知:如图,正比例函数的图象经过点P和点Q(-m,m+3),求m的值.
已知:如图,正比例函数的图象经过点P和点Q(-m,m+3),求m的值. 如图,正比例函数
如图,正比例函数 与二次函数y=-x2+2x+c的图象都经过点A(2,m).
与二次函数y=-x2+2x+c的图象都经过点A(2,m). 与二次函数y=-x2+2x+c的图象都经过点A(2,m).
与二次函数y=-x2+2x+c的图象都经过点A(2,m).