题目内容
抛物线y= x2-4x+k与x轴交于A、B两点(点B在点A的右侧),与y轴交于点C(0,6),动点P在该抛物线上.
x2-4x+k与x轴交于A、B两点(点B在点A的右侧),与y轴交于点C(0,6),动点P在该抛物线上.(1)求k的值;
(2)当△POC是以OC为底的等腰三角形时,求点P的横坐标;
(3)如图,当点P在直线BC下方时,记△POC的面积为S1,△PBC的面积为S2.试问S2-S1是否存在最大值?若存在,请求出S2-S1的最大值;若不存在,请说明理由.

【答案】分析:(1)把点C的坐标代入已知函数解析式y= x2-4x+k来求k的值;
x2-4x+k来求k的值;
(2)利用等腰三角形的“三合一”性质可知,点P是线段OC的垂直平分线与抛物线的交点;
(3)需要分类讨论,如图2、图3,根据点P所处的位置不同,可求得S2-S1=- m2+6m=-
m2+6m=- (m-2)2+6,然后由抛物线的开口方向,顶点坐标可以求得它的最值.
(m-2)2+6,然后由抛物线的开口方向,顶点坐标可以求得它的最值.
解答: 解:(1)⊙抛物线y=
解:(1)⊙抛物线y= x2-4x+k经过点C(0,6)
x2-4x+k经过点C(0,6)
∴ ×02-4×0+k=6
×02-4×0+k=6
解得k=6;
(2)如图1,过OC的中点D作y轴的垂线,当△POC是以OC为底的等腰三角形时,由OD= ×6=3可知,点P的纵坐标为3.
×6=3可知,点P的纵坐标为3.
由(1)可知,抛物线的解析式为y= x2-4x+6,
x2-4x+6,
令y=3得 x2-4x+6=3,解得x=4
x2-4x+6=3,解得x=4

∴点P的横坐标为4
 ;
;

(3)∵由(1)可知,抛物线的解析式为y= x2-4x+6
x2-4x+6
令x=0,得y=6;令y=0,得 x2-4x+6=0,
x2-4x+6=0,
解得 x1=2,x2=6.
∴点A、B、C坐标分别为(2,0)、(6,0)、(0,6),则OA=2,OB=OC=6
设点P为(m, m2-4m+6),当点P在直BC下方时0<m<6,
m2-4m+6),当点P在直BC下方时0<m<6,
过点P作PE⊥y轴于E,作直PG⊥x轴于G.
当2≤m<6时,如图2,
PE=m,PG= m2+4m-6,S2=S四边形COPB-S△POC,
m2+4m-6,S2=S四边形COPB-S△POC,
∵S四边形COPB=S△BOC+S△POB= ×OB×(OC+PG)=-
×OB×(OC+PG)=- m2+12m,
m2+12m,
2S1=OC×PE=6
∴S2-S1=S四边形COPB-2S1
=- +12m-6m=-
+12m-6m=- m2+6m;
m2+6m;
当0<m<2时,如图3.
PE=m,PG= m2+4m-6,S2=S△BOC+S△POB-S1
m2+4m-6,S2=S△BOC+S△POB-S1
同理可求S2-S1=- m2+6m
m2+6m
综上所述,当0<m<6时,S2-S1=- m2+6m=-
m2+6m=- (m-2)2+6.
(m-2)2+6.
∵抛物线S2-S1=- (m-2)2+6的开口方向向下,
(m-2)2+6的开口方向向下,
∴当m=2时,它有最大值.
∵m=2满足0<m<6,
∴当m=2时,S2-S1存在最大值6.
点评:本题综合考查了等腰三角形的性质、待定系数法求二次函数解析式以及三角形面积的求法.解答(2)题时,一定要分类讨论,以防漏解或错解.
 x2-4x+k来求k的值;
x2-4x+k来求k的值;(2)利用等腰三角形的“三合一”性质可知,点P是线段OC的垂直平分线与抛物线的交点;
(3)需要分类讨论,如图2、图3,根据点P所处的位置不同,可求得S2-S1=-
 m2+6m=-
m2+6m=- (m-2)2+6,然后由抛物线的开口方向,顶点坐标可以求得它的最值.
(m-2)2+6,然后由抛物线的开口方向,顶点坐标可以求得它的最值.解答:
 解:(1)⊙抛物线y=
解:(1)⊙抛物线y= x2-4x+k经过点C(0,6)
x2-4x+k经过点C(0,6)∴
 ×02-4×0+k=6
×02-4×0+k=6解得k=6;
(2)如图1,过OC的中点D作y轴的垂线,当△POC是以OC为底的等腰三角形时,由OD=
 ×6=3可知,点P的纵坐标为3.
×6=3可知,点P的纵坐标为3.由(1)可知,抛物线的解析式为y=
 x2-4x+6,
x2-4x+6,令y=3得
 x2-4x+6=3,解得x=4
x2-4x+6=3,解得x=4

∴点P的横坐标为4

 ;
;
(3)∵由(1)可知,抛物线的解析式为y=
 x2-4x+6
x2-4x+6令x=0,得y=6;令y=0,得
 x2-4x+6=0,
x2-4x+6=0,解得 x1=2,x2=6.
∴点A、B、C坐标分别为(2,0)、(6,0)、(0,6),则OA=2,OB=OC=6
设点P为(m,
 m2-4m+6),当点P在直BC下方时0<m<6,
m2-4m+6),当点P在直BC下方时0<m<6,过点P作PE⊥y轴于E,作直PG⊥x轴于G.
当2≤m<6时,如图2,
PE=m,PG=
 m2+4m-6,S2=S四边形COPB-S△POC,
m2+4m-6,S2=S四边形COPB-S△POC,∵S四边形COPB=S△BOC+S△POB=
 ×OB×(OC+PG)=-
×OB×(OC+PG)=- m2+12m,
m2+12m,
2S1=OC×PE=6
∴S2-S1=S四边形COPB-2S1
=-
 +12m-6m=-
+12m-6m=- m2+6m;
m2+6m;当0<m<2时,如图3.
PE=m,PG=
 m2+4m-6,S2=S△BOC+S△POB-S1
m2+4m-6,S2=S△BOC+S△POB-S1同理可求S2-S1=-
 m2+6m
m2+6m 综上所述,当0<m<6时,S2-S1=-
 m2+6m=-
m2+6m=- (m-2)2+6.
(m-2)2+6.∵抛物线S2-S1=-
 (m-2)2+6的开口方向向下,
(m-2)2+6的开口方向向下,∴当m=2时,它有最大值.
∵m=2满足0<m<6,
∴当m=2时,S2-S1存在最大值6.
点评:本题综合考查了等腰三角形的性质、待定系数法求二次函数解析式以及三角形面积的求法.解答(2)题时,一定要分类讨论,以防漏解或错解.

练习册系列答案
相关题目
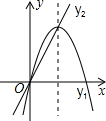 如图,抛物线y1=-x2+4x和直线y2=2x.当y1>y2时,x的取值范围是( )
如图,抛物线y1=-x2+4x和直线y2=2x.当y1>y2时,x的取值范围是( )| A、0<x<2 | B、x<0或x>2 | C、x<0或x>4 | D、0<x<4 |