题目内容
如图，AB为圆O的弦，点C在圆上，点D在AB上，且CA=CD，过点C作圆O的切线交BA的延长线于P，已知PA=2，BD=8，则AC为（ ）
A．2
B．3
C．4
D．5
【答案】分析：连接BC，利用已知条件证明△PAC∽△BDC，即可求出AC的长．
解答：
解：连接BC，
∵CA=CD，
∴∠1=∠2，
∴∠PAC=∠CDB，
∵PA是圆的切线，
∴∠PCA=∠B，
∴△PAC∽△CDB，
∴
，
∵PA=2，BD=8，
∴
，
∴AC2=16，
∴AC=4．
故选C．
点评：本题考查弦切角定理和相似三角形的判定以及相似三角形的性质的应用，解题的关键是添加辅助线构造相似三角形．
解答：
解：连接BC，∵CA=CD，
∴∠1=∠2，
∴∠PAC=∠CDB，
∵PA是圆的切线，
∴∠PCA=∠B，
∴△PAC∽△CDB，
∴
，∵PA=2，BD=8，
∴
，∴AC2=16，
∴AC=4．
故选C．
点评：本题考查弦切角定理和相似三角形的判定以及相似三角形的性质的应用，解题的关键是添加辅助线构造相似三角形．
练习册系列答案
相关题目
如图，AB为圆O的弦，点C在圆上，点D在AB上，且CA=CD，过点C作圆O的切线交BA的延长线于P，已知PA=2，BD=8，则AC为（ ）
如图，AB为圆O的弦，点C在圆上，点D在AB上，且CA=CD，过点C作圆O的切线交BA的延长线于P，已知PA=2，BD=8，则AC为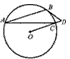
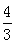，求CD的长。